СИЛА – причина изменения импульса (скорости) тела

Основу динамики, как Вам уже известно, из курса физики средней школы, составляют три закона Ньютона.

 

Первый закон Ньютона:

Существуют системы отсчета, в которых свободная материальная точка (тело) движется равномерно и прямолинейно или покоится. Такие системы отсчета называют инерциальными. Материальная точка (тело) называется свободной, если внешние воздействия компенсируют друг друга. Инерциальной является гелиоцентрическая система отсчета, связанная с Солнцем и тремя звездами, направления на которые взаимно перпендикулярны (это можно установить опытным путем). Всякая другая система, которая движется равномерно и прямолинейно или покоится относительно гелиоцентрической, тоже инерциальна. Система отсчета, связанная с Землей, не является инерциальной, потому что Земля вращается вокруг собственной оси и вокруг Солнца, но при изучении законов динамики неинерциальностью земной (геоцентрической) системы можно пренебречь.

 

Второй закон Ньютона

Хотя второй закон Ньютона традиционно записывают в виде: , сам Ньютон записывал его несколько иначе.

Второй закон Ньютона в современной формулировке звучит так: в инерциальной системе отсчета скорость изменения импульса материальной точки равна векторной сумме всех сил, действующих на эту точку.

где 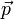− импульс материальной точки, 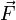− суммарная сила, действующая на материальную точку. Второй закон Ньютона гласит, что действие несбалансированных сил приводит к изменению импульса материальной точки.^[9]

По определению импульса:

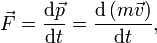
где − масса, 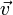− скорость.

По правилу нахождения производной произведения:

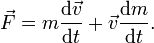
Если масса материальной точки остается неизменной, то производная по времени от массы равна нулю, и уравнение принимает вид:

Учитывая определение ускорения точки, второй закон Ньютона принимает вид:

Считается, что это «вторая самая известная формула в физике», хотя сам Ньютон никогда явным образом не записывал свой второй закон в этом виде.

Поскольку в любой инерциальной системе отсчёта ускорение тела одинаково и не меняется при переходе от одной системы к другой, то и сила инвариантна по отношению к такому переходу.

Во всех явлениях природы сила, независимо от своего происхождения, проявляется только в механическом смысле, то есть как причина нарушения равномерного и прямолинейного движения тела в инерциальной системе координат. Обратное утверждение, т.е установление факта такого движения, не свидетельствует об отсутствии действующих на тело сил, а лишь о том, что действия этих сил взаимно уравновешиваются. Иначе: их векторная сумма есть вектор с модулем, равным нулю. На этом основано измерение величины силы, когда она компенсируется силой, величина которой известна.

Второй закон Ньютона позволяет измерять величину силы. Например, знание массы планеты и ее центростремительного ускорения при движении по орбите позволяет вычислить величину силы гравитационного притяжения, действующую на эту планету со стороны Солнца.

Третий закон Ньютона

Для любых двух тел (назовем их тело 1 и тело 2) третий закон Ньютона утверждает, что сила действия тела 1 на тело 2, сопровождается появлением равной по модулю, но противоположной по направлению силы, действующей на тело 1 со стороны тела 2.^[12] Математически закон записывается так:

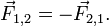
Этот закон означает, что силы всегда возникают парами «действие-противодействие». Если тело 1 и тело 2 находятся в одной системе, то суммарная сила в системе, обусловленная взаимодействием этих тел равна нулю:

Это означает, что в замкнутой системе не существует несбалансированных внутренних сил. Это приводит к тому, что центр масс замкнутой системы (то есть той, на которую не действуют внешние силы) не может двигаться с ускорением. Отдельные части системы могут ускоряться, но лишь таким образом, что система в целом остается в состоянии покоя или равномерного прямолинейного движения. Однако в том случае, если внешние силы подействуют на систему, то ее центр масс начнет двигаться с ускорением, пропорциональным внешней результирующей силе и обратно пропорциональным массе системы.

Основной закон динамики вращательного движения:

 или M=Je,

 

 где М - момент силы M=[ r · F ],

J -момент инерции

 

•-момент импульса тела.

 

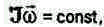^- если М (внешн)=0 - закон сохранения момента импульса.

- кинетическая энергия вращающегося тела.

     

 работа при вращательном движении.

 

Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения СИ: кг·м².

Обозначение: I или J.

Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.