Сейчас мы рассмотрим, как происходят колебания в электромагнитной волне. Пусть волна будет плоской, т.е. E и H не зависят от x и y.
Вернемся к уравнениям Максвелла:
 (1a)
(1a)
 (2a)
(2a)
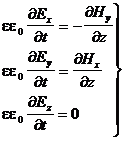 (3a)
(3a)
 (4a)
(4a)
Отсюда видно, что Hz и Ez не зависят от z и t, т.е они могут быть либо постоянными, либо равными нулю. Мы рассматриваем только изменяющиеся поля, т.е. можем положить их = 0.
Таким образом, мы получим, что изменяются только Ex, Ey и Hx, Hy. Это означает, что вектор E =Ex i +Ey j перпендикулярен направлению распространения света. Аналогично, вектор H перпендикулярен направлению распространения.
|
|
Как ориентирован вектор E и вектор H друг относительно друга? Из (1а) и (3а) мы видим, что Hx связано с Ey и Hy c Ex.
Если первоначально Ey = 0, т.е. было создано поле, которое меняется только вдоль оси Y, то оно создает поле Hx. Поле Hx создает поле Ey и т.д.
Таким образом векторы E, H, z образуют правую тройку.
Из (3а) возьмем  от 2-го уравнения:
от 2-го уравнения:

 или
или  (9)
(9)
Это частные случаи волнового уравнения. Из них следует, что зная вектор  всегда можно найти другой вектор —
всегда можно найти другой вектор —  . Это однозначное соответствие. Покажем это:
. Это однозначное соответствие. Покажем это:
Решение волнового уравнения.
До сих пор мы не конкретизировали вид функций E (x,y,z,t) и H (x,y,z,t). Особенно большое значение имеют гармонические или монохроматические волны. Простейшим решением волнового уравнения является функция:
Ey(z,t) = E0cos(wt-kz+a) (10)
H x(z,t) = H0cos(wt-kz+a) (11)
Подставим в уравнения Максвелла, учитывая что 


|
|

 (12)
(12)
Зная E, всегда можно найти H.
E, H, k — правая тройка.
Комплексные функции.
Здесь и далее мы будем представлять гармонические функции cos и sin в виде комплексных чисел. Вспомним некоторые свойства комплексных чисел
z 1 = x1+ iy1, z2 = x2 + iy2
Сумма: z = z 1 + z2 = (x1 +x2) + i(y1 +y2)
Re z = Re z1 + Re z2
Производная: 
Интеграл: 
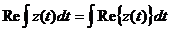
 .
.
Формула Эйлера: 
 2018-02-13
2018-02-13 749
749










