2018-02-13
2476
При наблюдении интерференционной картина с помощью бипризмы Френеля можно отметить, что, по мере удаления от центра, картина размывается. Отчетливо видно только несколько полос. Одна из причин уменьшения видимости полос в уменьшении степени когерентности складываемых волн в данной точке экрана (точке наблюдения). Полосы исчезают, когда складываемые волны становятся полностью некогерентны.
Наглядное объяснение этого явления представлено на рис.4. Предположим, что на экране видны первые три порядка интерференции (m=3), а затем полосы исчезают (рис.4). Исчезновение интерференционных полос при m>3 означает, что световые волны, пришедшие в точки экрана уже некогерентны. Следовательно, если разность хода лучей определяется интервалом DL ≤ l ког = 3l, то складываемые волны являются в какой то степени когерентны. Данное расстояние l ког, при смещении на которое две волны утрачивают когерентность, называют длиной когерентности. Таким образом, простейший способ оценки длины когерентности:
l ког ≈ mmax·l, (22)
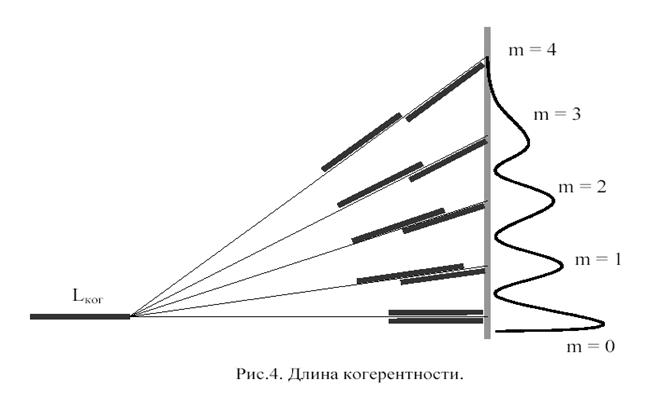
где mmax – максимальный порядок интерференции, соответствующий еще видимой светлой полосе.
Можно найти выражение, определяющее длину когерентности l ког. Учтем, что монохроматический свет – это идеализация. Реальный свет, даже прошедший через систему монохроматоров (светофильтров), остается в определенной степени немонохроматичным и содержит набор монохроматических компонент в конечном интервале длин волн (l, l+Dl). Для характеристики источников света используют величину – степень монохроматичности света l/Dl. Предположим, что эти монохроматические компоненты равномерно заполняют указанный интервал длин волн.
Из формулы (17) следует, что ширина интерференционной полосы Dy пропорциона
 |
льна длине волны l. На рис.5 показаны положения максимумов для длин волн, соответствующих крайним значениям интервала (l, l+Dl): сплошные отрезки – для l, пунктирные – для l + Dl. Максимумы от промежуточных длин волн заполняют интервал между крайними максимумами каждого порядка интерференции (области, выделенные темным цветом (рис.5)). В результате промежуточные максимумы, как видно на рис.5, будут постепенно (с ростом порядка интерференционного максимума) заполнять интервал между максимумами соседних порядков для l и l + Dl. Это приводит к постепенному размытию результирующих максимумов (нижний график на рис.5), т.е. к исчезновению интерференционных полос на экране.
Учитывая сказанное, из формулы (16а) для координат максимумов интенсивности ymax можно получить оценочное условие исчезновения полос:
m·(l + Dl) ≈ (m + 1)·l,
где m – предельный порядок интерференции, начиная с которого полосы исчезают, тогда:
mmax ≈ l/Dl. (23)
Таким образом, величину степени монохроматичности света l/Dl можно оценить по наибольшему порядку интерференционного максимума, наблюдаемого на экране.
Учитывая связь (22) предельного порядка интерференции mmax и длины когерентности l ког, используя (23) можно получить:
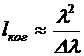. (24)
Например, у солнечного света l ког≈5l (~ 1,5 мкм), для одного из лучших (не лазерных) источников света – криптоновой (Kr) лампы l ког≈80 см, а у газового лазера (He-Ne) l ког≈ 2 км.
Таким образом, общее требование к оптическим установкам сводится к тому, что для получения отчетливой интерференционной картины оптическая разность хода световых волн DL должна быть меньше длины когерентности:
DL< l ког.
Длина когерентности связана со временем когерентности tког – промежутком времени, в течение которого случайные изменения фазы световой волны в данной точке достигают значения Dj»p. За это время волна распространяется на расстояние порядка длины когерентности:
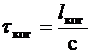. (25)
 |
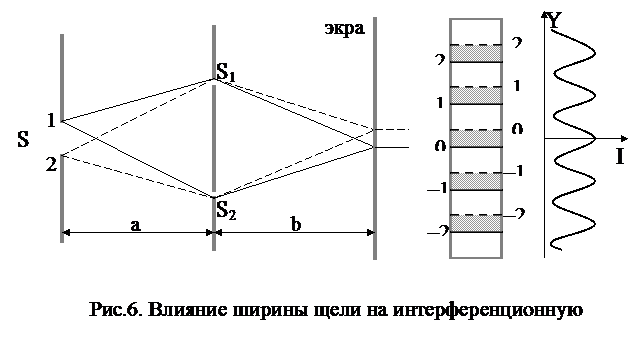Увеличение ширины D щели S в опыте с бипризмой Френеля (и в опыте Юнга (см. рис.6)), как и уменьшение степени немонохроматичности света приводит к ухудшению (размытию) интерференционной картины на экране. Для оценки такого влияния ширины щели на результат интерференции представим, что в опыте используется монохроматическое излучение, а щель S (рис.6) мысленно разобьем на совокупность более узких щелей. Пусть положение максимумов на экране от узкой щели, взятой около верхнего края щели S – точки 1 – таково, как показано на рис.6 сплошными линиями. А максимумы от узкой щели, взятой вблизи нижнего края щели S – точки 2, будут смещены вверх (на рис.6 они отмечены пунктирными линиями). Интервалы между этими максимумами заполнены максимумами от узких промежуточных щелей, расположенных между краями щели S (между точками 1 и 2).
При расширении щели S расстояния между максимумами от ее крайних элементов будут увеличиваться, т.е. интервалы между соседними максимумами от одного края щели будут постепенно заполняться максимумами от остальных элементов щели. Если расстояние от щели S до плоскости (S1S2) равно расстоянию от плоскости (S1S2) до экрана a = b, то при ширине D щели S, равной ширине интерференционной полосы D = Dy, интервал между соседними максимумами от края 1 будет целиком заполнен максимумами от остальных элементов щели, а значит, исчезнут интерференционные полосы на экране. Размытие наблюдаемых интерференционных полос можно объяснить и другим способом. Полосы размываются вследствие того, что вторичные источники S1 и S2 становятся некогерентными. Это позволяет ввести понятие радиуса когерентности rког, как максимальное поперечное направлению распространения волны расстояние, на котором возможно проявление интерференции. На рис.7 показана ширина когерентности:
hког = 2rког.
Для вычисления hког запишем условие, при котором щели S1 и S2 становятся некогерентными источниками: hког» d, где d – расстояние между щелями. Так как интерференционная картина исчезает, когда ширина щели примерно равна ширине полосы (D» DY), а ширина полосы равна Dy = lL/d, то:
hког» d = lL/Dy» lL/D
или
hког » l/j (26)
где j – угловая ширина щели S (см. рис.7).
Таким образом, ширина когерентности пропорциональна длине волны света и обратно пропорциональна угловой ширине источника относительно точки наблюдения.
 |
