Двухлучевая интерференция

Рассмотрим интерференцию, возникающую при наложении двух когерентных волн, для которых вектор колеблется в одном и том же направлении. и 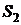– источники этих волн (рис. 1.). Пусть первая волна распространяется в среде с показателем преломления 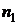, а вторая - в среде с показателем преломления . Из теории колебаний известно, что в тех точках пространства, где разность фаз 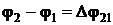складываемых колебаний удовлетворяет условию , будет наблюдаться максимальное усиление колебаний. Если же , то колебания будут в наибольшей степени ослабляться. Разность фаз складываемых колебаний в точке (рис. 1.) равна . Учитывая, что , разность фаз можно выразить как

, (7)

где . (8)

Скалярная величина называется оптической разностью хода волн 1 и 2.

Теперь условия усиления и ослабления света могут быть определены через оптическую разность хода двух когерентных волн:

1) условие усиления , . (9)

Интерференционный максимум будет наблюдаться, если на разности хода двух лучей укладывается целое число волн

2) условие ослабления 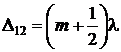, , (10)

Интерференционный минимум наблюдается, если на разности хода двух лучей укладывается полуцелое число волн.

1.4. Длина и время когерентности

Излучение любого обычного (не лазерного) источника не является строго монохроматическим. Каждый атом или молекула источника света излучает цуг волн (отдельный короткий импульс излучения) в течение промежутка времени, который называетсясредним временем жизни t излучающего атома. Для частот видимого света t 10^–8с. Протяженность цуга при этом имеет величину порядка 10⁷ длин волн l, и в первом приближении каждый такой цуг можно считать квазимонохроматичным. Однако при спонтанном излучении, которое осуществляется в обычных источниках света, электромагнитные волны испускаются атомами (молекулами) вещества независимо друг от друга, со случайным значением начальной фазы. Поэтому за время наблюдения D t >10^–8 с волны, спонтанно излучаемые атомами (молекулами) источника света, некогерентны и при наложении не интерферируют. Часть волны, сохраняющая примерное постоянство волновых характеристик, называется длиной когерентности l _ког, а время испускания цуга τ_ког временем когерентности. Очевидно, что длину цуга можно отождествить с длиной когерентности. Связь между l _коги τ_ког

.                                                                (11)

     Пусть спектральный интервал излучения, создающего наблюдаемую интерференционную картину, ограничен длинами волн λ иλ+Δλ. Интерференционная картина будет размываться, если максимум m -ого порядка для длины волны λ+Δλ будет накладываться на максимум (m +1)-го порядка для длины волныλ. Тогда с учетом условия максимума (1.9)

,                                     (12)

откуда                      .                                                           (13)

Таким образом, установлено значение предельного порядка интерференции, при котором интерференция исчезает, т.е. складываемые колебания становятся некогерентными.

     С другой стороны, интерференция наблюдается до тех пор, пока разность хода не превышает длину когерентности :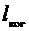

,                                           (14)

где m_max – максимальный порядок интерференции, соответствующий еще видимой светлой полосе.

Из (13) и (14) находим связь длины когерентности со степенью монохроматичности света 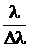  и длиной волны λ:

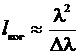                                                         (15)

Найдем оптическую разность хода D₁₂ лучей (на рис.2 величина оптической разности хода обозначена D) от источников S₁и S₂, приходящих в произвольную точку Р экрана.

Величину D₁₂ можно определить, зная координату y точки Р на экране, расстояние d между мнимыми источниками и расстояние L от источников до экрана. Из рассмотрения рис.2 следует:

r₁²= L²+ (у – d /2)²;

r₂²= L²+ (у + d /2)²,

или r₂²- r₁²= 2dу + d²/2» 2dу, т.к. d «у,

тогда D₁₂ = r₂- r₁= 2dу/(r₂+ r₁).

Вследствие невысокой степени монохроматичности света источников S₁ и S₂ интерференционная картина наблюдается только вблизи центра экрана, когда координата у «L. Поэтому можно считать r₁+ r₂» 2L и тогда

.                                                       (16)

Из формулы (16) можно определить координаты y интерференционных полос, получающихся при прохождении света через бипризму Френеля. Подставляя условия максимумов (9) и минимумов (10) интерференции в (16), соответственно получим:

координаты светлых полос:

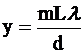, m = 0, ±1, ±2…,                        (16а)

координаты темных полос:

, m=0, ±1, ±2…,                     (16б)

где m - номер максимума или минимума.

Ширина интерференционной полосы Dу, т.е. расстояние между соседними минимумами или максимумами интенсивности света на любом участке интерференционной картины одинакова, и ее можно найти из соотношения

Dу= Ll/d,                                                       (17)

откуда

l = d × Dу/L,                                                 (18)

Для определения расстояния d между мнимыми источниками S₁ и S₂, можно воспользоваться собирающей линзой с известным фокусным расстоянием F (см. рис. 3).

Расположим линзу так, чтобы источники S₁ и S₂ лежали между фокусом F и двойным фокусом 2F. При этом их изображения S₁' и S₂' будут находиться на расстоянии l от линзы. Если поместить на этом расстоянии экран с масштабной линейкой, то по нему можно непосредственно найти расстояние d´ между изображениями источников.

Из подобия треугольников ВО'F и OFS₁´ находим

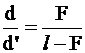
или

.                                                (19)

Из подобия треугольников S₁O'B и OO'S₁´ следует, что



.                                                 (20)

Решая совместно уравнения (9) и (10), можно найти:

.                                                (21)

Подставляя в формулу (18) значения d и L из выражений (19) и (21), получим расчетную формулу для определения длины световой волны с помощью бипризмы Френеля

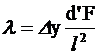.                                             (22)