Контрольной работы № 1

Задачи 1.1, 1.2 решаются с использованием основного уравнения гидростатики

р = р₀ + ρgh = р₀ + hγ, (3.1)

где р₀- давление, приложенное к поверхности жидкости, Па;

γ – удельный вес жидкости,, Н/м³.

При помощи уравнения (3.1) можно определить давление в любой точке покоящейся жидкости. Это давление, складывается из двух величин: давления р₀ на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости.

Из основного уравнения гидростатики видно, что какую бы точку в объеме всего сосуда мы не взяли, на нее всегда будет действовать давление, приложенное к внешней поверхности жидкости р₀.

Другими словами давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости по всем направлениям одинаково.

Это положение известно под названием закона Паскаля. Поверхность, во всех точках которой давление одинаково, называется п оверхностью уровня. В обычных условиях поверхности уровня представляют собой горизонтальные плоскости.

Задачи по определению гидростатического давления решаются

следующим образом:

1. На чертеже обозначают линии равного давления.

2. Определив поверхность с известным давлением, находят давление на следующей поверхности, применяя уравнение (3.1).

3. Решают уравнение относительно искомого параметра.

Предположим, что необходимо определить манометрическое давление в трубопроводе, заполненном водой (рисунок 3.1). К трубопроводу присоединен жидкостный манометр. Высота столба ртути в манометре h₂ = 25 см. Центр трубопровода (точка А) расположен на h₁ = 40 см ниже линии раздела между водой и ртутью.

Линия равного давления пройдет по точкам В и С. Находим давление в точке В. Точка В расположена выше точки А на величину h₁, следовательно, давление в точке В будет равно

. (3.2)

В точке С давление будет такое же, Рисунок 3.1

как в точке В

. (3.3)

Определим давление в точке C, подходя, справа

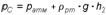. (3.4)

Приравнивая правые части уравнений (3.3) и (3.4), получаем

. (3.5)

Отсюда манометрическое давление в трубопроводе

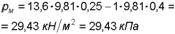(3.6)

Задача 1.3. Как уже отмечалось выше, поверхность, во всех точках которой давление одинаково, называется поверхностью уровня или поверхностью равного давления. При неравномерном или непрямолинейном движении на частицы жидкости кроме силы тяжести действуют еще и силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.

Рассмотрим пример такого относительного покоя.

Определим поверхности уровня в жидкости, находящейся в цистерне, в то время как цистерна движется по горизонтальному пути с постоянным ускорением a (рисунок 3.2).

К объему жидкости массой m в этом случае приложены ее вес G = mg и сила инерции P_u, равная по величине ma. Равнодействующая этих сил направлена к вертикали под углом α, тангенс которого равен 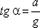Рисунок 3.2

Так как свободная поверхность, как поверхность равного давления, нормальна к указанной равнодействующей, то она в данном случае представит собой уже не горизонтальную плоскость, а наклонную, составляющую угол α с горизонтом.

Учитывая, что величина этого угла зависит только от величины ускорения, приходим к выводу, что положение свободной поверхности не будет зависеть от рода находящейся в цистерне жидкости.

Любая другая поверхность уровня в жидкости также будет плоскостью, наклоненной к горизонту под углом α. Если бы движение цистерны было не равноускоренным, а равнозамедленным, направление ускорения изменилось бы на обратное, и наклон свободной поверхности обратился бы в другую сторону (рисунок 3.2, пунктир).

Задача 1.4. Решение задач с применением уравнения Л. Эйлера для покоющейся идеальной жидкости можно производить в приведенной последовательности:

1. Разместить рассматриваемый объем жидкости в пространственной системе координат.

2. Приложить все действующие на жидкость массовые (сила тяжести и инерции) и поверхностные (сила давления) силы.

3. Записать уравнение Л.Эйлера для рассматриваемой задачи.

4. Найти уравнение свободной поверхности.

5. Решить уравнение относительно искомой величины.

Рассмотрим часто встречающийся в практике случай относительного покоя жидкости во вращающихся сосудах (например, в сепараторах и центрифугах, применяемых для разделе ния жидкостей). В этом случае (рисунок 3.3) на любую частицу жидкости при ее относительном равновесии действуют массовые силы: сила тяжести

G = mg, Н (3.7)

и центробежная сила

P_u = mω²r, Н, (3.8)

где r - расстояние от частицы до

оси вращения, м;

ω - угловая скорость вращения

сосуда, с^-1.

Поверхность жидкости нормальна в Рисунок 3.3

каждой точке к равнодействующей

этих сил R. Уравнение Л.Эйлера, применительно к задаче, примет вид

Проинтегрируем уравнение Л.Эйлера

_._(3.9)

Для точки 0, x=0, у = 0, z = h, p = p_a, тогда постоянная интегрирования

С = p_a + и уравнение примет вид

Необходимо также помнить, что x = y =r, а x²+ y² = r².

Из чертежа находим

. (3.10)

С другой стороны:

, (3.11)

где z - координата точки, расположенной на поверхности жидкости на

расстоянии r от оси вращения.

Таким образом, получаем:

, (3.12)

откуда

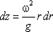, (3.13)

или после интегрирования

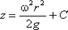. (3.14)

В точке пересечения кривой АСВ с осью вращения r = 0, z = h. Следовательно, постоянная интегрирования С = h, тогда уравнение свободной поверхности жидкости:

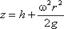, (3.15)

т.е. кривая АСВ является параболой, а свободная поверхность жидкости параболоидом. С учетом полученного уравнения можно определить искомые значения неизвестных в задаче величин, если принять к сведению, что объем параболоида вращения:

, (3.16)

где r – координата точки на свободной поверхности жидкости, соответствующая координате z.

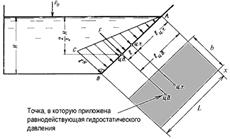
Задача 1.5, 1.6. Пусть мы имеем резервуар с наклонной стенкой, заполненный жидкостью удельным весом γ. Ширина стенки в направлении, перпендикулярном плоскости чертежа, равна b (рисунок. 3.4). Стенка условно показана развернутой относительно оси АВ и заштрихована на рисунке. Построим график изменения избыточного гидростатического давления на стенку АВ.

Так как избыточное гидростатическое давление изменяется по линейному закону P = γgh, то для построения графика, называемого эпюрой давления, достаточно найти давление в двух точках, например А и B.

Избыточное гидростатическое давление в точке А будет равно

р_A = γh = γ·0 = 0. (3.17)

Давление в точке В:

р_B = γh = γH. (3.18)

Рисунок 3.4

где H - глубина жидкости в резервуаре.

Согласно первому свойству гидростатического давления, оно всегда направлено по внутренней нормали к поверхности воздействия. Следовательно, гидростатическое давление в точке В, величина которого равна γH, направлено перпендикулярно к стенке АВ. Соединив точку А с концом отрезка γH, получим треугольную эпюру распределения давления АВС с прямым углом в точке В. Среднее значение давления будет равно

. (3.19)

Если площадь наклонной стенки S = bL, то равнодействующая гидростатического давления равна

, (3.20)

где h_c = Н/2 - глубина погружения центра тяжести плоской поверхности под линию свободной поверхности жидкости.

Однако, точка приложения равнодействующей силы гидростатического давления ц.д. не будет совпадать с центром тяжести плоской поверхности. Эта точка находится на расстоянии е от центра тяжести и равна отношению момента инерции площадки относительно центральной оси к статическому моменту этой же площадки.

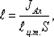(3.21)

где J_Аx - момент инерции площади S относительно центральной оси, параллельной Аx.

В частном случае, когда стенка имеет форму прямоугольника размерами b и l и одна из его сторон лежит на свободной поверхности с атмосферным давлением, центр давления (ц.д.) находится на расстоянии l/3 от нижней стороны площадки.

Задача 1.7, 1.8. Для определения силы гидростатического давления на криволинейную поверхность необходимо выполнить расчет в следующей последовательности:

Разместить объем рассматриваемой жидкости в пространственной системе координат.
Приложить все действующие на криволинейную поверхность силы.
Определить положение пьезометрической плоскости.
Определить равнодействующую силу гидростатического давления.
Определить положение центра тяжести и линию действия равнодействующей силы гидростатического давления.

Пусть жидкость заполняет резервуар, правая стенка которого представляет собой цилиндрическую криволинейную поверхность АВС, перпендикулярную плоскости чертежа (рисунок 3.5), ширина поверхности АВС (размер, уходящий за плоскость чертежа) b.

Плоскость свободной поверхности с атмосферным давлением на ней, является пьезометрической плоскостью.

Если в условии задачи нет линии свободной поверхности, то положение пьезометрической плоскости (плоскости, проходящей по показаниям пьезометров) находим, отложив от точки подключения манометра вертикально вверх расстояние Рисунок 3.5

равное

h_p₌ р/γ, (3.22)

где р – давление в точке подключения манометра.

Объем жидкости в отсеке АОСВ находится в равновесии. Это значит, что силы, действующие на поверхности выделенного объема V, и силы веса взаимно уравновешиваются.

Схема к определению равнодействующей гидростатического давления на цилиндрическую поверхность Предположим, что выделенный объем V

представляет собой твердое тело того же удельного веса, что и жидкость (объем заштрихован).

Левая поверхность этого объема – вертикальная проекция криволинейной поверхности АВС на плоскость yOz (на чертеже вертикальная стенка АО) имеет площадь

S_z = bH, (3.33)

Если спроецировать криволинейную поверхность АВС на вертикальную плоскость yOx, то получим проекцию площадью S_x= ОС b _.

Cила избыточного гидростатического давления на площадь S_x, равна

F_x = γ S_zh_c, (3.34)

где h_c – глубина погружения центра тяжести вертикальной проекции S_z под линией свободной поверхности (пьезометрической плоскостью).

С правой стороны на отсек будет действовать реакция R цилиндрической поверхности. Реакцию R разложим на две составляющие R_x и R_z.

Из действующих поверхностных сил осталось учесть только давление на свободной поверхности р₀.

На объем АВСО будет действовать сила веса жидкости

G = γV, (3.35)

направленная вертикально вниз.

Спроецируем все силы на ось Ох:

F_x - R_x = 0 откуда F_x = R_x = γ S_уh_c. (3.36)

Теперь спроецируем все силы на ось Оz:

R_z - G = 0 откуда R_z = G = γV, (3.37)

где V- объем тела давления, это объем, заключенный между криволинейной поверхностью, линиями, проецирующими ее на пьезометрическую плоскость и самой пьезометрической плоскостью.

Составляющая силы гидростатического давления по оси O_y обращается в нуль, значит R_y = F_y = 0.

Таким образом, реакция цилиндрической поверхности в общем случае равна

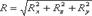. (3.38)

а поскольку реакция цилиндрической поверхности равна равнодействующей гидростатического давления R=F, то делаем вывод, что

. (3.39)

Точка приложения равнодействующей силы гидростатического давления находится на расстоянии эксцентриситета от центра тяжести вертикальной проекции криволинейной поверхности S_z_.Эта точка носит название – центр давления (ц.д.). Величина эксцентриситета е определяется уравнением

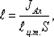(3.40)

где J_А_y - момент инерции площади S_яотносительно центральной оси, параллельной Оy;

S_я= S, L_ц.т.= h_c.(3.41)

Задача 1.9, 1.10. Задачи, решение которых основано на законе Паскаля, можно решать с применением основного уравнения гидростатики:

р = р₀ + ρgh = р₀ + hγ. (3.42)

Закон Паскаля является следствием основного уравнения гидростатики. Давление, приложенное к поверхности жидкости, передается без изменения всем точкам жидкости и по всем направлениям.

При этом необходимо помнить, что сила давления равна произведению давления, оказываемого на площадку, на площадь этой площадки.

Р = р S. (3.43)

Задачи с использованием закона Паскаля можно решать по следующей схеме:

1. Приложить все действующие на поршни силы.

2. Записать уравнения для определения этих сил.

3. Решить уравнения относительно неизвестного.

Задача 1.11, 1.12. Задачи с использованием в ходе решения закона Архимеда решаются следующим способом:

Прикладываем все силы, действующие на плавающее тело.
Составляем необходимое количество уравнений, равное количеству неизвестных.
Решаем систему уравнений относительно искомой величины.

На тело, погруженное в жидкость или газ действует выталкивающая сила (P_А), численно равная весу жидкости в объеме погруженной части тела (V_п.ч.т.).

P_А = ρ_жg V_п.ч.т.

(3.44)

Сила направлена вертикально вверх и приложена в центре водоизмещения. Центр водоизмещения – центр тяжести погруженной части тела.

Для однородного тела плавающего на поверхности справедливо соотношение

(3.45)

где: V - объем плавающего тела;
ρ _m - плотность тела.

ρ_m / ρ_ж - относительная плотность тела.

Существующая теория плавающего тела довольно обширна, поэтому мы ограничимся рассмотрением лишь гидравлической сущности этой теории.

Запасом плавучести называют силу, равную весу жидкости в объеме надводной части плавающего тела.

Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние называется остойчивостью. Условия остойчивости выполняются, если центр тяжести лежит ниже центра водоизмещения и если оба центра в условии равновесного плавания лежат на одной вертикальной прямой – оси плавания.

Вес жидкости, взятой в объеме погруженной части судна называют водоизмещением, а точку приложения равнодействующей давления (т.е. центр давления) - центром водоизмещения. Объем погруженной части тела называют – объемом водоизмещения (V_п.ч.т.). При нормальном положении судна центр тяжести С и центр водоизмещения d лежат на одной вертикальной прямой O'-O", представляющей ось симметрии судна и называемой осью плавания (рисунок 3.6). Плоскость пересечения поверхности тела с плоскостью свободной поверхности называют плоскостью плавания.

Пусть под влиянием внешних сил судно наклонилось на некоторый угол α, часть судна KLM вышла из жидкости, а часть K'L'M', наоборот, погрузилось в нее. При этом получили новое положении центра водоизмещения d'. Приложим к точке d' подъемную силу R и линию ее действия продолжим до пересечения с осью симметрии O'-O". Полученная точка m называется метацентром, а отрезок mC = h_м(расстоянии от центра тяжести до метацентра) называется метацентрической высотой. Метацентрическую высоту можно рассчитать при помощи уравнения:

h_м = (I_s / V_п.ч.т) – е, (3.46)

где I_s – центральный момент инерции площади

плоскости плавания относительно продольной оси.

е – эксцентриситет (расстояние между центром тяжести и центром водоизмещения).

Будем считать h_м положительной, если точка М лежит выше точки C, и отрицательной - в противном случае.

Теперь рассмотрим условия равновесия судна:

если h > 0, то судно возвращается в Рисунок 3.6

1) первоначальное положение;
2) если h = 0, то это случай безразличного равновесия;
3) если h < 0, то это случай неостойчивого равновесия, при котором продолжается дальнейшее опрокидывание судна.

Следовательно, чем ниже расположен центр тяжести и, чем больше метацентрическая высота, тем больше будет остойчивость судна.

Задача 1.13. В процессе истечения жидкости из резервуаров через отверстия и насадки (короткие трубки различной формы) в атмосферу или пространство, заполненное газом или той же жидкостью потенциальная энергия, которой обладает жидкость, находящаяся в резервуаре, преобразуется в кинетическую энергию свободной струи.

Основным вопросом, который интересует в данном случае, является определение скорости истечения и расхода жидкости для различных форм отверстий и насадков.

Рассмотрим большой резервуар с жидкостью под давлением р₀, имеющий малое круглое отверстие в стенке на достаточно большой глубине Н₀ от свободной поверхности

Жидкость вытекает в воздушное пространство с давлением р₁. Отверстие выполнено в толстой стенке, но с заострением выходной кромки. Струя, отрываясь от кромки отверстия, несколько сжимается. Такое сжатие обусловлено изменением движения жидкости от радиального вдоль стенки, к осевому в струе. Рисунок 3.7

Степень сжатия струи оценивается коэффициентом сжатия

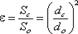, (3.47)

где S_с и S_о - площади поперечного сечения струи и отверстия соответственно;

d_с и d_о - диаметры струи и отверстия соответственно.

Скорость истечения жидкости через отверстие

, (3.48)

где Н - напор, определяется как

, (3.49)

φ- коэффициент скорости

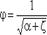, (3.50)

где α - коэффициент Кориолиса;
ζ- коэффициент сопротивления отверстия.

Расход жидкости определяется как произведение действительной скорости истечения на фактическую площадь сечения:

, (3.51)

Произведение ε и φ принято называть коэффициентом расхода, т.е.

μ = εφ.

В итоге получаем расход

, (3.52)

где ΔР - расчетная разность давлений, под действием которой происходит истечение.

Значение коэффициента сжатия ε, сопротивления ζ,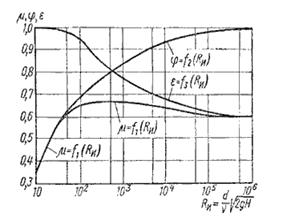

скорости φ и расхода μ для круглого отверстия можно определить по эмпирически построенным зависимостям. На рисунке 3.8 показаны зависимости коэффициентов ε, ζ и μ от числа Рейнольдса,

подсчитанного для скорости идеальной жидкости

Рисунок 3. 8

, (3.53)

где ν - коэффициент кинематической вязкости, м²/с.

Если жидкость истекает не в атмосферу, а в пространство, заполненное этой же жидкостью (рисунок 3.9), то такой случай называется истечением под уровень, или истечением через затопленное отверстие.

В этом случае вся кинетическая энергия струи теряется на вихреобразование, как при внезапном расширении.

Скорость истечения в сжатом сечении струи

, (3.54)

где φ - коэффициент скорости;
Н - расчетный напор,

Рисунок 3. 9

. (3.55)

Расход жидкости равен

(3.56)

Таким образом, имеем те же расчетные формулы, что и при истечении в атмосферу, только напор Н в данном случае представляет собой разность гидростатических напоров по обе стороны стенки, т.е. скорость и расход жидкости в данном случае не зависят от высот расположения отверстия.

Внешним цилиндрическим насадком называется короткая трубка длиной,

равной (3,5-7) диаметров (рисунок 3.10).

Скорость и расход жидкости, истекающей через насадок, определяется по тем же формулам, что и через отверстие. Коэффициент расхода μ, зависящий от относительной длины насадка l / d и числа Рейнольдса, и коэффициент скорости φ определяется по справочнику в зависимости от формы насадка[2]. Рисунок 3.10

Задача 1.14. Рассмотрим случай опорожнения открытого в атмосферу сосуда при постоянно изменяющемся напоре, при котором течение является неустановившемся (рисунок 3.11).

Однако если напор, а следовательно, и скорость истечения изменяются медленно, то движение в каждый момент времени можно рассматривать как установившееся, и для решения задачи применить уравнение Бернулли.

Пусть переменная высота уровня жидкости Рисунок 3.11

в сосуде h, площадь поперечного сечения резервуара на этом уровне S, площадь отверстия S_о. Запишем уравнение для определения объема, вытекающего из резервуара за промежуток времени dt:

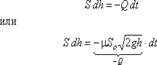, (3.57)

где dh - изменение уровня жидкости за время dt.

Отсюда время полного опорожнения сосуда высотой Н

. (3.58)

Если будет известен закон изменения площади S по высоте h, то интеграл можно подсчитать. Для призматического сосуда S = const, следовательно, время его полного опорожнения

. (3.58 а)

Из этого выражения следует, что время полного опорожнения призматического сосуда в два раза больше времени истечения того же объема жидкости при постоянном напоре, равном первоначальному.

Задача 1.15, 1.16. Задачирешаются с применением уравнения Бернулли. Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости (рисунок 3.12) уравнение Бернулли имеет следующий вид:

(3.59)

Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:

(3.60)

и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная. С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии: z₁ и z₂ - удельные энергии положения, характеризующие потенциальную энергию в сечениях 1-1 и 2-2;
- удельные энергии давления, характеризующие потенциальную энергию давления в тех же сечениях;
- удельные кинетические энергии в тех же сечениях. Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна.

Уравнение Бернулли можно истолковать и чисто геометрически. Дело в том, что каждый член уравнения имеет линейную размерность. Глядя на рисунок 3.12, можно заметить, что

z₁ и z₂- геометрические высоты сечений 1-1 и 2-2 над плоскостью сравнения;

- пьезометрические высоты;

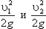- скоростные высоты в указанных сечениях.

В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная. Рисунок 3. 12

Уравнение Бернулли для

потока реальной жидкости несколько отличается от уравнения

(3.61)

При движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии

Потерянная энергия или потерянный напор обозначаются и имеют

также линейную размерность. Уравнение Бернулли для реальной жидкости имеет вид:

(3.62)

Из рисунка 3.12 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1-1 и 2-2.

Два коэффициента α₁ и α₂, которые называются коэффициентами Кориолиса и зависят от режима течения жидкости (α = 2 для ламинарного режима, α = 1 для турбулентного режима).

Потерянная высота 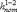складывается из линейных потерь, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)

= h_пот + h_м (3.63)

гдеh_пот - потери напора по длине, м.

h_м - потери на местные сопротивления, м.

, (3.64)

где λ - коэффициент гидравлического трения, который для ламинарного потока вычисляется по выражению:

, (3.65)

Где R_e – число Рейнольдса, которое служит для определения режимов движения жидкости.

Ламинарным называется слоистое течение без перемешивания частиц жидкости и без пульсации скорости и давления. При ламинарном течении жидкости в прямой трубе постоянного сечения все линии тока направлены параллельно оси трубы, при этом отсутствуют поперечные перемещения частиц жидкости.

Турбулентным называется течение, сопровождающееся интенсивным перемешиванием жидкости с пульсациями скоростей и давлений. Наряду с основным продольным перемещением жидкости наблюдаются поперечные перемещения и вращательные движения отдельных объемов жидкости. Переход от ламинарного режима к турбулентному наблюдается при определенной скорости движения жидкости. Эта скорость называется критической υ _кр.

Значение этой скорости прямо пропорционально кинематической вязкости жидкости и обратно пропорционально диаметру трубы.

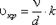, (3.66)

где ν - кинематическая вязкость, м²/ с.
k - безразмерный коэффициент;
d - внутренний диаметр трубы, м.

Входящий в эту формулу безразмерный коэффициент k, одинаков для всех жидкостей и газов, а также для любых диаметров труб. Этот коэффициент называется критическим числом Рейнольдса Re_кр и определяется следующим образом:

. (3.67)

Как показывает опыт, для труб круглого сечения Re_кр примерно равно 2320. Таким образом, критерий подобия Рейнольдса позволяет судить о режиме течения жидкости в трубе. При Re < Re_кр течение является ламинарным, а при Re > Re_кр течение является турбулентным.

Точнее говоря, вполне развитое турбулентное течение в трубах устанавливается лишь при Re примерно равно 4000, а при Re = 2300…4000 имеет место переходная, критическая область.

Режим движения жидкости напрямую влияет на степень гидравлического сопротивления трубопроводов. Если число Рейнольдса лежит в диапазоне 4000 < Re < 10(d / Δ _э) коэффициент λ определяется по полуэмпирической формуле Блазиуса

. (3.68)

Для определения существует также эмпирическая формула П.К. Конакова, которая применима для гидравлически гладких труб

(3.69)

Во второй области, расположенной между линий II и пунктирной линией справа, коэффициент λ зависит одновременно от двух параметров - числа Re и относительной шероховатости Δ/r₀, которую можно заменить на Δ_э. Для определения коэффициента λ в этой области может служить универсальная формула А.Д. Альтшуля:

, (3.70)

где Δ_э - эквивалентная абсолютная шероховатость, м.

Характерные значения Δ_э (в мм) для труб из различных материалов приведены в ПРИЛОЖЕНИИ А:

Третья область - область больших Re и Δ/r₀, где коэффициент λ не зависит от числа Re, а определяется лишь относительной шероховатостью (область расположена справа от пунктирной линии). Это область шероховатых труб, в которой все линии с различными шероховатостями параллельны между собой. Эту область называют областью автомодельности или режимом квадратичного сопротивления, т.к. здесь гидравлические потери пропорциональны квадрату скорости.

Определение λ для этой области производят по упрощенной формуле Шифринсона:

(3.71)

или по формуле Прандтля - Никурадзе:

. (3.72)

Коэффициент гидравлического трения можно получить из графика Никурадзе (рисунок 3.13).

Потери напора, определяемые по формуле Вейсбаха-Дарси, можно

определить,

Рисунок 3.13

зная коэффициент гидравлического сопротивления, который определяется в зависимости от числа Рейнольдса Re и от эквивалентной шероховатости Δ_э. Для удобства сводные данные по определению λ представлены в ПРИЛОЖЕНИИ А.

Потери напора на местные сопротивления определяются в зависимости от вида местного сопротивления по уранению

. (3.73)

Это выражение является следствием теоремы Борда, которая гласит, что потеря напора при внезапном расширении русла равна скоростному напору, определенному по разности скоростей.

Выражение (1 - S₁/S₂)² обозначается греческой буквой ζ (дзета) и называется коэффициентом потерь, таким образом

. (3.74)

Полная потеря напора в случае внезапного сужения определится по формуле

, (3.75)

где коэффициент сопротивления для сужения трубопровода определяется по полуэмпирической формуле И.Е. Идельчика:

, (3.76)

где n = S₁/S₂ - степень сужения.

При выходе трубы из резервуара больших размеров, когда можно считать, что S₂/S₁ = 0, а также при отсутствии закругления входного угла, коэффициент сопротивления ζ _суж = 0,5.

Потери напора в случае постепенного сужение русла (данное местное сопротивление представляет собой коническую сходящуюся трубу, которая называется конфузором) потери напора определяюся при помощи уравнения

, (3.77)

где коэффициент сопротивления конфузора определяется по формуле

, (3.78)

в которой n = S₁/S₂ - степень сужения.

При внезапном повороте (колено) потери тем больше, чем больше угол δ. Потерю напора рассчитывают по формуле

, (3.79)

где ζ _кол - коэффициент сопротивления колена круглого сечения, который определяется по графику в зависимости от угла колена δ (рисунок 3.14).

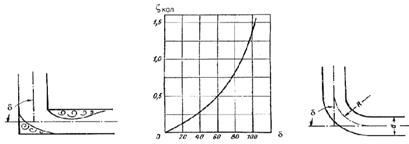
Рисунок 3.14

Плавность поворота значительно уменьшает интенсивность вихреобразования, а следовательно, и сопротивление отвода по сравнению с коленом. Это уменьшение тем больше, чем больше относительный радиус кривизны отвода R / d.

Коэффициент сопротивления отвода ζ _отв зависит от отношения R / d, угла δ, а также формы поперечного сечения трубы.

Для отводов круглого сечения с углом δ= 90 и R/d 1 при турбулентном течении можно воспользоваться эмпирической формулой:

. (3.80)

Для углов δ 70° коэффициент сопротивления

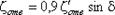, (3.81)

а при δ 100°

, (3.82)

Потеря напора в колене определится как

. (3.83)

Местные сопротивления трубопроводной арматуры можно определить по справочной литературе [2].

С помощью уравнения Бернулли решается задачи в следующей последовательности:

1. Выбирают два сечения по длине потока 1-1 и 2-2, таким образом, чтобы для одного из них были известны величины р, , g, а для другого сечения один или несколько параметров подлежали определению.