Уравнение первого начала для замкнутого пространства

Термодинамическая работа для всех простых тел определяется как работа изменения объёма

    

Рассмотрим замкнутую систему, к которой подводится тепло при постоянном объёме. Так как объём не меняется, то термодинамическая работа равна нулю и тогда

             

 

               (5.6)

Таким образом, теплота, подводимая к замкнутой ТС, тратится только на увеличение внутренней энергии.

Пусть тело перешло из состояния 1 в состояние 2 тогда  , но в изохорном процессе ()  

               тогда

             (5.7)     Следовательно, изменение внутренней энергии не зависит от вида процесса изменения состояния рабочего тела, а зависит только от начальной и конечной температуры этого тела. Т.к. удельная внутренняя энергия идеального газа является параметром состояния, то уравнение (5.7) действительно для её вычисления в любом термодинамическом процессе.

    При перемещении рабочего тела из области одного давления в область другого используется понятие потенциальной работы.

 известно, что между  и 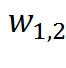 существует взаимосвязь

В данном случае уравнение первого начала термодинамики примет вид

   

сгруппируем члены уравнения

 (а)  В термодинамике принято называть

     U+рV=Н – массовой энтальпией рабочего тела – потенциальной энергетической возможностью тела [Дж].

Удельная массовая энтальпия рабочего тела

      h=u+р  [Дж/кг]                 (5.8)    

она, как и внутренняя энергия является также параметром состояния, т.к. в правой части уравнения все члены – параметры состояния.

Подставим (5.8) в уравнение (а)

          (5.9)           уравнение (5.9) является уравнением 1-го начала при перемещении рабочего тела из области одного давления в область другого.     

 

Рассмотрим поток рабочего тела по каналу произвольной формы между сечениями 1 и 2. В соответствии с уравнением неразрывности массовый расход газа через сечения постоянен (G=const). Потенциальная работа, возникшая из-за разности давлений в сечениях, идёт на:

q

-изменение кинетической энергии потока                         

/2– /2;                                                                        -на изменение уровня высоты сечения 2 по отношению к сечению 1 g(z₂–z);                          -на совершение внешней работы w*₁,₂;               -на преодоление сил трения в потоке .                                                                    

     подставим (5.10) в уравнение (5.9)

 (5.11).

Уравнение (5.11)– запись 1-го начала термодинамики для потока, используется для описания движения газа по трубопроводам.

Если внешняя работа не совершается, а трением можно пренебречь, то               (5.12)   В условиях, когда движения нет, то р₁=р₂, т.е. всё тепло идёт на изменение энтальпии газа         (5.13).

 

Закон Майера

1кг

1кг

 

 

Рассмотрим 1кг рабочего тела при р=const и V=const.

В условиях постоянного объёма  (а)

В условиях постоянного давления                  (б)                                     (в)                        величина подведённого тепла при р=соnst  (г)

Подставим в (б) значения из (г), (а), (в)

 

При изменении температуры на 1 градус          или (5.14)

(5.14) носит название закона Майера.

Из уравнения (5.14) видно, что изобарная теплоёмкость больше изохорной теплоёмкости на величину удельной газовой постоянной. Т.к. R не зависит от параметров состояния, то теплоёмкость идеального газа не зависит от давления и объёма, а лишь от температуры.

Умножив (5.14) на молярную массу μ получим                                                                         (5.15)

Разность молярных удельных теплоём таже.

Рассмотрим отношение удельных массовых теплоёмкостей, называемое показателем адиабаты                                                                      к>1    (5.16)

Решим совместно (5.14) и (5.16) получим                         

В большинстве случаев показатель адиабаты определяется природой газа и не зависит от температуры:

–для одноатомных газов к=1,67                              –для 2-х атомных газов к=1.4                                 –для 3-х и многоатомных к=1,28.