2018-02-14
963
Частным случаем рассмотренных выше линейных однородных дифференциальных уравнений являются ЛОДУ с постоянными коэффициентами.
Пусть дано ЛОДУ второго порядка
,
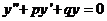Где p и q постоянны.
Для нахождения общего решения уравнения 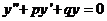достаточно найти два его частных решений, образующих фундаментальную систему.
Будем искать частные решения уравнения 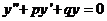в виде
,
где k – некоторое число. Дифференцируя эту функцию 2 раза и подставляя выражения для у, у’ и у’’ в уравнение 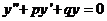, получим: 
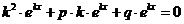, т.е.
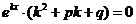, или 
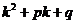=0 (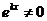
).
Уравнение 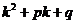=0 (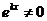) называется характеристическим уравнением ДУ .
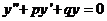При его решении возможны следующие три случая
Случай 1: Корни уравнения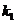 
и 
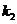уравнения 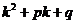=0 (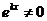). Действительные и различные: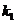 
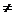
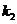(D =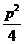 
- q > 0).
В этом случае частными решениями уравнения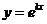 
являются функции 
= 
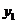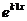
и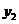 
= 
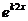. Они образуют фундаментальную систему решений (линейно независимы), т.к. их вронскиан
W(x) =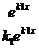 
= 
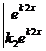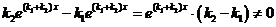
Следовательно, общее решение уравнения ,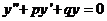
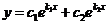
Случай 2: Корн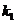и и 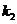характеристического уравнения 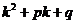=0 (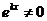), действительные равные: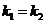 
.
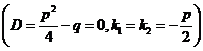В этом случае имеем лишь одно частное решение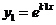 
.
Покажем, что наряду с 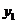решением уравнения 
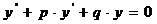будет и 
.
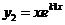Действительно, подставим функцию 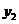в уравнение 
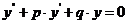. Имеем: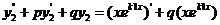 
+
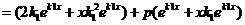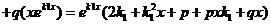
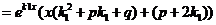
Но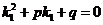 
, т.к. 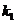есть корень уравнения 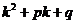=0 ();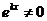 
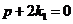, т.к. по условию 
.
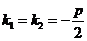Поэтому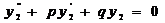 
, т.е. функция 
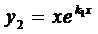является решением уравнения .
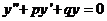Частные решения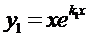 
и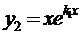 
образуют фундаментальную систему решений: 
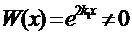. Следовательно, в этом случае общее решение ЛОДУ 
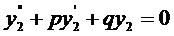имеет вид
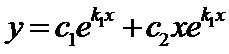
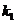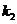Случай 3: Корни и уравнения 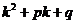=0 (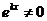) комплексные: 
, 
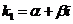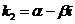
В этом случае частными решениями уравнения 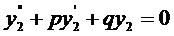являются функци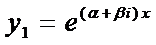и 
и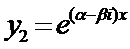 
.
По формулам Эйлера:
, 
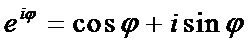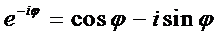
Имеем
,
.
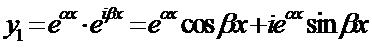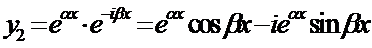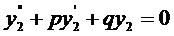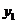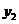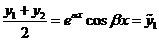Найдем два действительных частных решения уравнения . Для этого составим две линейные комбинации решений для и :
и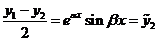 
.
Функци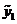и 
и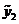 
являются решениями уравнения 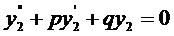, что следует из свойств решений ЛОДУ второго порядка. Эти решения 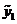и 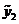образуют фундаментальную систему решений, т.к. 
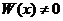. Поэтому общее решение данного уравнения запишется в виде 
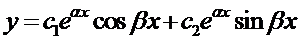или
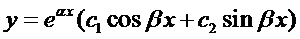
Линейные неоднородные дифференциальные уравнения (ЛНДУ)
