2018-02-14
241
Рассмотрим ЛНДУ 
. Его общим решением является функция, т.е.
Частное решение 
уравнения можно найти, если известно общее решение 
соответствующего однородного уравнения 
, методом вариации произвольных постоянных, состоящим в следующем. Пусть 
– общее решение уравнения .
Заменим в общем решении постоянные 
и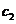 
неизвестными функциями 
и 
и подберем их так, чтобы функция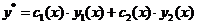 
была решением уравнения .
Найдем производную
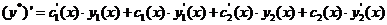
Подберем функции и так,чтобы 
Тогда 
,
.
Подставляя выражение для , 
, 
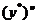в уравнение , получим:
+
,
или
+
Поскольку 
и 
– решения уравнения , то выражения в квадратных скобках равны 0, а потому 
.
Таким образом, функция 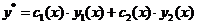будет частным решением уравнения , если функции и удовлетворяют системе уравнений и :
Определитель системы 
, так как это определитель Вронского для фундаментальной системы частных решений и уравнения . Поэтому система имеет единственное решение 
и 
, где 
и 
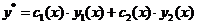- некоторые функции от х. Интегрируя эти функции, находим и , а затем по формуле составляем частное решение уравнения .
