Линейные однородные дифференциальные уравнения второго порядка

 

Рассмотрим ЛОДУ второго порядка:

И установим некоторые свойства его решений.

 

Теорема:

Если функци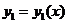и  и 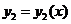 являются частными решениями уравнения , то решением этого уравнения является также функция

                           ,

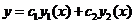где  и 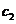 - произвольные постоянные.

 

Подставим функцию 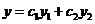 и ее производные в левую часть ЛОДУ .

Получаем: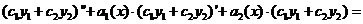

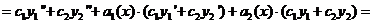
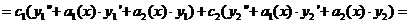
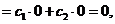
так как функци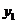и  и 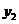- решения уравнения  и, значит, выражения в скобках тождественно равны 0.

Таким образом, функция 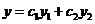также является решением уравнения .

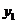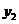Из теоремы, как следствие, вытекает, что если  и  - решения уравнения ,

То решениями его будут также функции у= 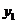+  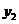 и у=с .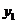

Функция 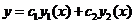 содержит две произвольные постоянные и является решением уравнения .

 

А для ответа на вопрос, может ли эта функция являться общим решением, введем понятие линейной зависимости и линейной независимости функций.

Функци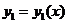и и 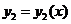называются линейно независимыми на интервале (a;b), если равенство

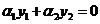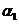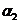
, где , R, выполняется тогда и только тогда, когда 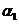= =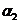0.

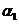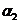Если хотя бы одно из чисел или  отлично от 0 и выполняется равенство 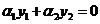, то функции  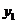и 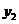называются линейно зависимыми.

 

Средством изучения линейной зависимости системы функций является так называемый определитель Вронского или вронскиан.

Для двух дифференцируемых функци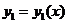й и 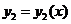вронскиан имеет вид

              W(x)= .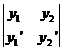

Имеют место следующие теоремы.

Теорема: Если дифференцируемые функци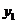и (х) и 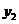(х) линейно зависимы на (a;b), то определитель Вронского на этом интервале тождественно равен 0.

 

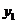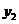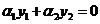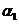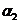Так как функции  и  линейно зависимы, то в равенстве  значение или  отлично от 0. Пусть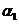 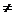0, тогда 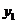= 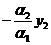; поэтому для любого х (a;b)

 

 

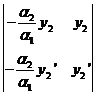           W(x)= =0.

 

Теорема: Если функци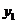и (х) и 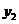(х) - линейно независимые решения уравнения  на (a;b), то определитель Вронского на этом интервале нигде не обращается в нуль.

 

 

Интегрирование ДУ второго порядка с постоянными коэффициентами