2018-02-14
455
Пусть в некоторую точку 
приходят световые волны от двух источников 
, причем частота колебаний светового вектора одинакова в обеих волнах.
Запишем для колебаний в точке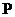 
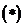
Пусть колебания световых векторов 
происходят вдоль одного и того же направления. В этом случае для амплитуды результирующих колебаний можно записать:
.
Пусть волны распространяются в одной и той же среде. Перейдем к интенсивности
,
.
Сложение некогерентных световых волн.
Обозначим разность фаз колебаний в точке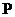
.
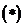
В случае естественных источников света второе слагаемое есть случайная функция времени
.
Если первое слагаемое 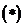сравнимо с величиной 
, то и все выражение случайным образом изменяется со временем
.
Следовательно, для точки 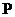с координатами 
, запишем
.
С точки зрения измерения интенсивности как функции времени следует учитывать, что реальные приборы характеризуются так называемым быстродействием 
.
Быстродействие прибора - это минимальное время, в течение которого возможна регистрация изменения измеряемой величины.
Обозначим:
- характерное время случайного изменения разности фаз колебаний 
.
Как правило, при измерении интенсивности световой волны выполняется условие
.
При этом прибор регистрирует не мгновенное значение интенсивности, а среднее за время измерение значения интенсивности
.
Обозначим далее
.
При случайном обрыве и возобновлении колебаний разность фаз изменяется совершенно беспорядочно, многократно пробегает за время измерения все значения от 0 до 
. При этом 
также многократно и случайно пробегает всевозможные значения от 
до 
, так что интеграл стремится к нулю.
Следовательно,
.
Это соотношение справедливо для любых точек 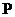в пространстве.
При сложении некогерентных световых колебаний во всех точках пространства интенсивность результирующих колебаний одна и та же и постоянна во времени.
.
