Вопрос 3. Циклические коды

Важным частным случаем линейных блоковых кодов являются циклические коды (а значительная часть линейных блоковых кодов эквивалентна им).

Они могут быть относительно легко реализованы и обладают специфической и довольно хорошо понятой математической структурой, основанной на математическом аппарате линейных рекуррентных последовательностей.

Подпространство V наборов длины п называется циклическим подпространством или циклическим кодом, если для любого век­тора v = (а_n-1, а_n-2,..., а₀) из подпространства V вектор v’ = (а₀, а_n-1, а_n-2,..., а₁), получаемый в результате циклического сдвига компонент вектора v на единицу вправо, также принадле­жит подпространству V.

Циклические коды строятся на алгебре многочленов.

Вторым свойством всех разрешенных комбинаций циклических кодов является их делимость без остатка на некоторый специальным образом выбранный[2] полином степени r  – G (x), называемый производящим.

Синдромом ошибки в этих кодах является наличие остатка от деления принятой кодовой комбинации на производящий полином.

Эти свойства используются при построении кодов, кодирующих и декодирующих устройств, а также при обнаружении и исправлении ошибок.

Здесь     k – количество информационных символов,

              r – количество проверочных символов.

n = к + r.

По полиному G(x) строится порождающая матрица линейного кода.

В теории циклических кодов доказывается, что порождающими могут быть только такие полиномы, которые являются делителями двучлена (бинома) Xⁿ –1

G(x)×H(x) = xⁿ – 1,

для q = 2

G(x)×H(x) = xⁿ + 1,                                 (3.1)

где H(x) – некоторый полином, степени n – r не обязательно неприводимый, он порождает проверочную матрицу.

Справка. Собственно, как составное число раскладывается на произведение простых чисел, так и многочлен xⁿ + 1 раскладывается на произведение неприводимых многочленов меньшей степени, один из которых и берется за G(x), а произведение остальных – H(x).

Из выражения (3.1) следует, что xⁿ + 1 делится на G(x).

По определению, если кодовая комбинация длины n записанная в виде

принадлежит коду, то и

тоже принадлежит коду.

Проверим это.

Чтобы получить , надо коэффициенты многочлена сдвинуть влево на одну позицию, т.е. 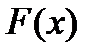умножить на x и переставить коэффициент в крайнюю правую позицию, для чего вычесть 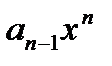 (в двоичном поле можно не вычесть, а прибавить), и прибавить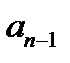

.

Чтобы 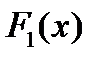 принадлежал коду, достаточно, чтобы он делился на G(x) нацело.

По определению F(x) делится на G(x) нацело, значит и  тоже.

 также делится на G(x), т.к. xⁿ + 1 делится на G(x) – см. выше (3.1).

Значит 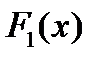 делится на G(x) нацело.

 

Кодирование.

Пусть последовательность информационных элементов длины k

а₀, а₁, …, а_i, …,а_k-1

представляется в виде полинома от формальной переменной x степени k – 1

.

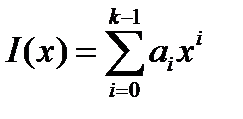Далее I (x) умножается на одночлен x^r степени r и делится на G (x) – производящий полином. Не нацело.

                           (3.2) 

где R (x) – остаток от деления т.е.

Здесь C(x) – той же степени, что и I(x).

Пример деления:

Перенесем в (3.2) дробь из правой части в левую

                               (3.3)

Обе части умножим на G (x)

                                           (3.4)

Коэффициенты полинома F(x) и есть последовательность символов помехоустойчивой кодовой комбинации длины n = k + r.

Полином F(x) без остатка делится на G(x). Если в F(x) закралась ошибка, он не поделится нацело на G(x) и остаток будет синдромом, позволяющим обнаружить, а при достаточной степени r и устранить ошибку.

Если представить 

                                    (2.4)

то F(x) будет выглядеть неразделимым.

Если представить 

                                      (2.4)

то видно, что F(x) будет разделимым, в нем старшие k разрядов будут информационными, а младшие r разрядов – проверочными, т.к. умножение информационного k-разрядного полинома I(x) на x^r

перенесут k разрядов полинома I(x) влево на r разрядов. А младшие r разрядов заполнятся операцией

Пример.

Пусть I = 1011

G(x) = x⁴ Å x Å 1

x^r = x³

Тогда             I(x) = x³ Å x Å 1

              I(x) ∙ x^r = x⁶ Å x⁴ Å x³

 

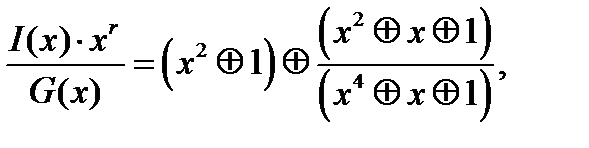
C(x) = x² Å 1,

проверка       

= (x⁴ Å x Å 1)(x² Å 1) Å x² Å x Å 1 = x⁶ Å x⁴ Å x³

Еще коды:

Среди циклических кодов особое место занимает класс кодов, предложенных

Боузом и Чоудхури и независимо от них Хоквингемом. Коды Боуза—Чоудхури-Хоквингема получили сокращённое наименование БЧХ- коды.

БЧХ- коды являются обобщением кодов Хемминга на случай исправления нескольких независимых ошибок (e_и > 1). Частными случаями БЧХ- кодов являются коды Файра, предназначенные для обнаружения и исправления серийных ошибок ("пачек" ошибок), код Голея - код, исправляющий одиночные, двойные и тройные ошибки (d min=7), коды Рида-Соломона (РС- коды), у которых символами кода являются многоразрядные двоичные числа.

 

В.КНЯЗЕВ

[1] 1. Перестановка любых двух строк, 2. Умножение любой строки на ненулевой элемент поля, 3. Прибавление произведения одной из строк матрицы на ненулевой элемент поля к другой строке матрицы.

[2] Неприводимый в данном поле полином – т.е. полином, который не может быть представлен в виде произведения многочленов низших степеней в данном поле.