Вопрос 2. Коды Хэмминга

Двоичный код Хэмминга (Ричард Уэсли Хэмминг –Richard Wesley Hamming), систематический код, имеет кодовое расстояние d = 3 и позволяет обнаруживать и исправлять одиночную ошибку.

Корректирующие коды обозначают (n,k), где n – количество символов в кодовой комбинации, из них k – количество информационных символов.

Коды Хэмминга для r проверочных символов

 r = 3, 4, 5, …

т.е. (7, 4), (15, 11), (31,26) и т.д.

Построение кодов Хэмминга основано на принципе проверки на четность числа единичных символов: каждый проверочный символ представляет собой сумму по модулю 2 некоторой подпоследовательности информационных символов.

Рассмотрим варианты кода Хэмминга для r = 3.

Вариант 1.

Пусть

Тогда для преобразования

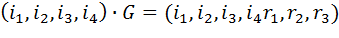
нужна матрица

,

 а по теореме 2.1. (о проверочной матрице)

.

Само преобразование

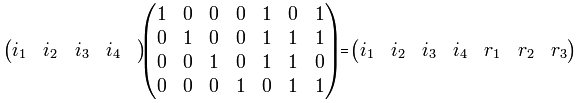
В декодере строится вектор-синдром (S ₁, S ₂, S ₃)

Если синдром равен «0» т.е. (0, 0, 0), то это означает, что ошибки нет.

Если синдром отличен от нуля, то по таблице синдромов можно найти позицию ошибки:

Рассмотрим еще один вариант, который иногда только и называется кодом Хэмминга (т.е. предыдущий вариант в этом смысле – не код Хэмминга).

Код сначала зададим при помощи его проверочной матрицы.

Рассмотрим матрицу Н из нулей и еди­ниц, содержащую m = 3 строки и 2^m — 1= 7 столбцов, причем столбцами являются все ненулевые двоичные наборы длины т, записанные так, что номер столбца записан в двоичной системе счисления в этом столбце

,

 

Число проверочных символов со­ставляет r = 3, число информационных символов равно 4, а общее количество бит в кодовой комбинации = 7.

Код по определению является разделимым (систематическим), т.е. в нем явным образом заданы информационные и проверочные символы.

Можно было бы задать например I₁I₂I₃I₄P₁P₂P₃, но так делать нецелесообразно.

Кодирование легко проводится, если в качестве проверочных вы­браны первый, второй и четвертый символы, так как в этом случае каждый из этих символов входит только в одно из проверочных соотношений, задаваемых матрицей Н. Т.е. используют следующую последовательность: P₁P₂I₁P₃I₂I₃I₄.

Чтобы рассчитать P₁P₂ и P₃, следует решить следующую систему уравнений, которая при данной последовательности распадается на отдельные уравнения.

 

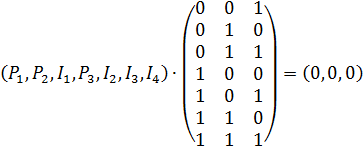
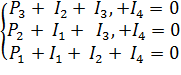
Откуда

Если при принятой нами проверочной матрице H взять последовательность I₁I₂I₃I₄P₁P₂P₃, то система не распадется на три независимых уравнения.

Полученные уравнения для P₁P₂P₃ позволяют воссоздать порождающую код матрицу G

 

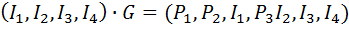
Рассмотрим обнаружение ошибок.

Предположим, что передавался кодовый вектор u и появилась одна ошибка. Тогда будет получен вектор u + е, где е — вектор, содержащий «1» в том разряде, где произошла ошибка, и «0» во всех остальных разрядах.

Синдром равен

 

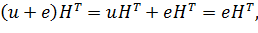
так как u — кодовый вектор и поэтому принадлежит нулевому пространству матрицы Н и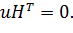

Но поскольку е — вектор, содержащий единственную единицу в разряде, соответствующем ошибке, то синдром еН^Т равен как раз той строке матрицы Н^Т, которая соот­ветствует ошибке.

Таким образом, сравнивая синдром с матрицей Н^Т, можно найти положение ошибки и затем исправить ее, просто заменив соответствующий символ на правильный.

Особенно удобно это делать, если использовать в качестве i-гo столбца матрицы Н двоичное представление числа i. Тогда для каждой отдельной оди­ночной ошибки синдром является двоичным представлением но­мера разряда, в котором произошла ошибка. Это расположение первоначально использовано Хэммингом.

Пример. Чтобы закодировать информационные символы 1100, нужно определить проверочные символы в слове P₁ P₂ 1 Р₃ 1 0 0. Кодовый вектор равен 0111100.

Предположим, что пятый символ принят ошибочно, тогда будет получен вектор 0111000. Легко вычислить синдром, который оказывается равным 101 — величине, соответ­ствующей пятому столбцу матрицы Н и указывающей на то, что ошибка произошла в пятом символе полученного вектора. Синдром является двоичным кодом числа 5, поскольку каждый столбец матрицы Н выбирался как двоичное представление номера столбца.

Существует понятие расширенный код Хэмминга. для q ≥ 2.