Истечение жидкости через насадки

Насадком называется короткая труба длиной 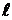 = (3–4) d ци­линд­рической, конической или коноидальной форм. Присоединение насадка к отверстию в тонкой стенке изменяет вытекающий из со­су­да расход и оказывает влияние на время опорожнения сосуда, даль­ность полета струи и т.д. Аналогичное явление наблюдается при ис­те­чении из отверстия в толстой стенке, т.е. когда .

Характер течения жидкости, ее толщина в различных насадках имеет много общего. Рассмотрим истечение жидкости через внешний цилинд­рический насадок (насадок Вентури) (рис. 8.5).

При наличии острой кромки возникает сжатие струи на входе в насадок. Максимальное сжатие образуется на расстоянии от плос­кости входа в отверстие, равном 0,5 d.

Площадь сжатого сечения потока w_с = ew, причем числовое зна­чение коэффициента сжатия зависит от условий входа. В частности, для рассматриваемого случая (круглое отверстие с острой кромкой) приближенно можно принять e = 0,64.

После сжатого сечения струя расширяется, заполняя полностью сечение, выходя из него полным сечением. Рассмотрим соотношение скоростей и давлений в сжатом сечении и на выходе из насадка (см. рис. 8.5). Давление на выходе из насадка равно ат­мо­сферному, а скорость – меньше скорости в сжатом сечении. Тогда, со­глас­но уравнению Бернулли, давление в сжатом сечении должно быть меньше атмосферного, т.е. в сжатом сечении образуется вакуум.

Рис. 8.5

Наличие в сжатом сечении вакуума существенно меняет картину истечения. В этом случае жидкость из резервуара изливается в об­ласть ва­куума, что сопоставимо с увеличением напора и объясняет уве­личе­ние действительного расхода. Для доказательства найдем расчетные зависимости для скорости истечения и расхода жидкости через насадок.

Запишем уравнение Бернулли для сечений 1–1 и 2–2. При сле­дующих условиях истечения:

1. Движение жидкости в насадке установившееся.

2. Входная кромка круглого отверстия – острая, что приводит к сжа­­тию струи, коэффициент сжатия .

3. На выходе из насадка струя заполняет все сечение (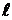 =3...4 d), поэтому e = 1.

4. Распределение давления в сечении 2–2 подчиняется гидроста­ти­ческому закону:

.

5. Коэффициент Кориолиса a = 1

                                                     (8.23)

Из анализа уравнения (8.23) в соответствии с расчетной схе­мой имеем:

;

,

где  – потери напора на участке  пренебрежительно малы;  – потери напора на входе до сжатого сечения;  –  потери напора на расширение струи (по теореме Борда).

С учетом малости потерь напора на участке  по уравнению Бернулли имеем:

                                                                  (8.24)

Применяя уравнение расхода для сжатого и выходного сечений

и исключая из уравнения (8.24), получим

.

Отсюда

              ,              (8.25)

где  – коэффициент скорости.

При  и коэффициент скорости равен j = 0,82.

Общий коэффициент сопротивления для насадка

.

Определяем расход из уравнения неразрывности с учетом, что , получим

.

Обозначая  и считая, что w₂ = w, получаем

                                                         ,                                 (8.26)

где  – коэффициент расхода насадка.

Так как для насадка e = 1, то m = j = 0,82. Сравнивая коэффициенты расхода и скорости для насадка и отверстия в тонкой стенке, видим, что насадок увеличивает расход и уменьшает скорость истечения.

Действительно, для больших значений Rе отношения

то есть расход через насадок увеличивается более чем на 35 % по сравнению со скоростью истечения из отверстия.

8.5. Зависимость коэффициентов истечения
от числа Рейнольдса

Полученные выше значения коэффициентов истечения для от­верстий и насадков различной формы справедливы для условий, когда влияние вязкости жидкости на истечение не проявляет себя в заметной степени.

Число Рейнольдса для истекающей струи вычисляется по формуле:

                                                        (8.27)

При числе Rе₀ > 10⁵ влияние вязкости можно не учитывать.

При Rе₀ > 3∙10⁵ (область, наиболее характерная для истечения из отверстий воды) практически остается неизменным.

Вместе с тем, коэффициент истечения зависит от числа Rе при ис­течении воды и других маловязких жидкостей из отверстий малого диаметра.

Кроме того, зависимость коэффициента расхода m от числа Рей­нольд­са необходимо учитывать при определении времени опорож­нения  сосудов.

При малых значениях Rе < 10 применима зависимость:

.

Для определения значений m при  применяется эмпирическая формула

                                                   ,                       (8.28)

где  – число Рейнольдса для насадка.

Из графика (рис. 8.6), построенного по формуле (8.28), видно, что при Re_н ® ¥ и m ® 0,813, что незначительно отличается от m = 0,82 для цилиндрического насадка.

Рис. 8.6

На графике (см. рис. 8.6) кривая 1 – соответствует случаю истечения из отверс­тия в тон­кой стенке, а кривая 2 – из цилиндрического насадка при . Из графика следует, что при Re_н < 1000 применение насадка умень­шает коэффициент расхода по сравнению с истечением из отверстия при одинаковых d.