 Виділимо на плоскій бічній стінці судини (рис. 10), нахиленої під кутом
Виділимо на плоскій бічній стінці судини (рис. 10), нахиленої під кутом  , довільну фігуру площею
, довільну фігуру площею 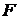 і визначимо діючу на неї з боку рідини силу тиску
і визначимо діючу на неї з боку рідини силу тиску  . Для наочності сполучимо розглянуту стінку з площиною креслення (тобто повернемо її на
. Для наочності сполучимо розглянуту стінку з площиною креслення (тобто повернемо її на  навколо осі
навколо осі  ).
).
Тому що тиск рідини в різних по висоті крапках площі 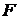 різний, то виділимо на цій площі елементарну площадку, що знаходиться на відстані
різний, то виділимо на цій площі елементарну площадку, що знаходиться на відстані 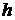 чи від вільної поверхні рідини
чи від вільної поверхні рідини 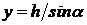 від осі
від осі  . Для такої нескінченно малої площі тиск у всіх її крапках однаковий і дорівнює
. Для такої нескінченно малої площі тиск у всіх її крапках однаковий і дорівнює 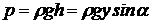 , отже, сила тиску рідини на елементарну площадку буде
, отже, сила тиску рідини на елементарну площадку буде 
Сила тиску на всю розглянуту площу 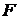 буде
буде 
 Вираження
Вираження  являє собою статичний момент розглянутої площі щодо осі
являє собою статичний момент розглянутої площі щодо осі  , що дорівнює добутку площі
, що дорівнює добутку площі 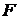 на відстань від її центра ваги до осі
на відстань від її центра ваги до осі  , тобто
, тобто 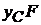 . Таким чином,
. Таким чином,  чи, заміняючи
чи, заміняючи  , одержимо
, одержимо
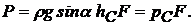 (33)
(33)
З (33) видно, що сила тиску рідини на плоску стінку  дорівнює добутку змоченою рідиною площі стінки
дорівнює добутку змоченою рідиною площі стінки 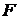 на гідростатичний тиск у її центрі ваги
на гідростатичний тиск у її центрі ваги  .
.
Якщо на вільну поверхню рідини діє тиск, відмінне від атмосферного, силу тиску на стінку можна знайти по формулах:
 (34)
(34)
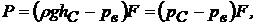 (35)
(35)
де  і
і  – відповідно манометричний тиск і вакуум на вільній поверхні рідини.
– відповідно манометричний тиск і вакуум на вільній поверхні рідини.
У ряді випадків, крім значення сили тиску рідини на стінку, необхідно знати координати крапки її додатка – центра тиску.
Припустимо, що сила тиску  прикладена в крапці
прикладена в крапці 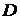 , що знаходиться від осі
, що знаходиться від осі  на відстані
на відстані  . Відповідно до теореми Вариньона про момент рівнодіючої (момент рівнодіючої сили щодо якої-небудь осі дорівнює сумі моментів складових сил щодо тієї ж осі)
. Відповідно до теореми Вариньона про момент рівнодіючої (момент рівнодіючої сили щодо якої-небудь осі дорівнює сумі моментів складових сил щодо тієї ж осі)  чи
чи  Замінивши в останнім вираженні
Замінивши в останнім вираженні  і
і  їх значеннях, одержимо
їх значеннях, одержимо  . Винесемо постійні за знак інтеграла і скоротимо їх
. Винесемо постійні за знак інтеграла і скоротимо їх 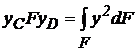 . Вираження
. Вираження  являє собою момент інерції площі фігури щодо осі
являє собою момент інерції площі фігури щодо осі  –
–  , що може бути виражений через момент інерції
, що може бути виражений через момент інерції  щодо центральної осі, рівнобічної осі
щодо центральної осі, рівнобічної осі  , у такий спо-
, у такий спо-
сіб:  . Тоді
. Тоді  , відкіля
, відкіля
 (36)
(36)
З (36) видно, що центр тиску для плоскої стінки знаходиться завжди нижче її цента ваги. Горизонтальна координата центра тиску  знаходиться на осі симетрії площі фігури.
знаходиться на осі симетрії площі фігури.
В окремому випадку, коли  тобто для горизонтального дна судини, відстань від вільної поверхні до центра ваги площі
тобто для горизонтального дна судини, відстань від вільної поверхні до центра ваги площі  буде дорівнює висоті рідини в судині
буде дорівнює висоті рідини в судині  , тому сила тиску рідини на дно судини
, тому сила тиску рідини на дно судини  . З цього вираження видно, що різні за формою судини, що мають однакові площі дна і заповнені однаковою рідиною на ту саму висоту, будуть мати однакову силу тиску на дно незалежно від форми судини і кількості рідини, що знаходиться в ньому, (гідравлічний парадокс). Центр тиску, для дна судини збігається з центром ваги площі.
. З цього вираження видно, що різні за формою судини, що мають однакові площі дна і заповнені однаковою рідиною на ту саму висоту, будуть мати однакову силу тиску на дно незалежно від форми судини і кількості рідини, що знаходиться в ньому, (гідравлічний парадокс). Центр тиску, для дна судини збігається з центром ваги площі.
 2018-02-14
2018-02-14 732
732








