Основне рівняння гідростатики

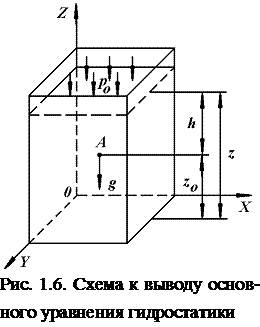
Розглянемо рідину, укладену в нерухомій судині (рис. 6) і, що знаходиться в поле дії сили ваги. Осі координат розташовані таким чином, щоб вісь 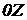 була спрямована нагору, тобто паралельно лінії дії сили ваги.

Усередині розглянутого обсягу рідини виділимо крапку 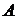, що знаходиться на відстані  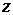від горизонтальної  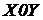площини чи на глибині  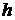від вільної поверхні рідини. Проекції одиничних масових сил на координатні осі в даному випадку будуть: 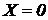, , 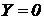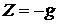. Підставляючи ці значення в рівняння рівноваги рідини (25), одержимо  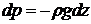чи після інтегрування 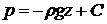, де 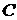 – постійна інтегрування.

Для визначення постійної інтегрування задамося початковими умовами: на вільній поверхні рідини, тобто пр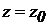и  (чи 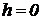), тиск 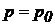, отже, 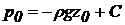, відкіля 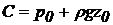. Підставимо знайдене значення  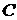в отримане посля інтегрування вираження

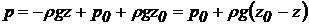
чи

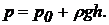                                                                                      (27)

Основне рівняння гідростатики (27) виражає залежність тиску в даній крапці спочиваючої рідини від роду рідини і відстані крапки від вільної поверхні. У цьому рівнянні 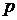 – абсолютний тиск (тиск, при вимірі якого за початок відліку приймають абсолютний нуль тиску) у даній крапці рідини,  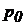– абсолютний тиск навколишнього середовища (зовнішній тиск на вільну поверхню рідини),  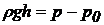– надлишковий тиск (тиск стовпа рідини) у даній крапці.

 

Абсолютний, манометричний і вакуумметричний

Тиск у рідині

У відкритих судинах, водоймах абсолютним тиском навколишнього середовища є атмосферний тиск 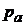. Оскільки атмосферний тиск (нормальна його величина 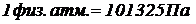) може мінятися, краще застосовувати термін барометричний тиск  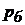(під ним розуміють тиск, рівне  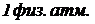з можливими відхиленнями). Для цих випадків рівняння (27) буде мати вид

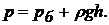                                                                                      (28)

Якщо абсолютний тиск у даній крапці рідини більше барометричного (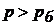), то останній член рівняння (28) визначає манометричний тиск

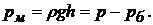                                                                            (29)

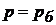
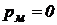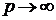
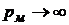Манометричний тиск являє собою надлишок тиску в даній крапці над барометричним. З рівняння (29) можна визначити межі виміру манометричного тиску: при , при , тобто значення манометричного тиску може змінюватися від  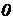до .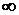

Якщо абсолютний тиск у даній крапці рідини менше барометричного (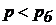), то останній член рівняння (28) визначає вакуум чи тиск розрядження

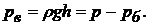                                                                             (30)

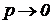
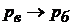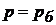
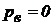Вакуум чи вакуумметричний тиск являє собою недолік тиску в даній крапці до барометричного. Межі виміру вакууму можуть бути встановлені з вираження (1.30): при , при , тобто значення вакуумметричного тиску може мінятися від  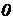до .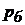

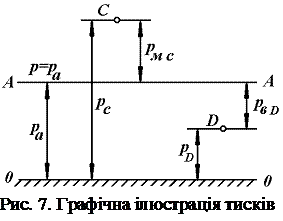Проілюструємо графічно все сказане вище про вакуумметричний, манометричний й абсолютний тиск. Уявимо собі площину, у всіх крапках якої абсолютний тиск 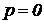. Слід цієї площини зображений на рис. 7 горизонтальною лінією 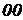;  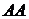– слід площини, абсолютний тиск у всіх крапках якої дорівнює атмосферному  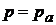чи барометричний 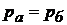. Таким чином, лінія  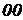є базою для відліку абсолютного тиску, а лінія  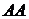– базою для відліку манометричного і вакуумметричного тиску.

Відстань від крапки 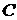 до лінії  являє собою абсолютний тиск у цій крапці 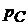, а відстань від крапки  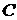до лінії  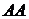– манометричний тиск у цій крапці .

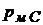Аналогічна відстань від крапки 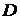 до лінії  являє собою абсолютний тиск у цій крапці 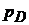, а відстань від крапки  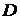до лінії  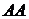– вакуумметричний тиск у цій крапці .

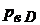Приведена на рис. 7 схема дає також наочне представлення про межі виміру манометричного і вакуумметричного тиску, що були установлені вище з виражень (29) і (30).

 

Сполучені судини

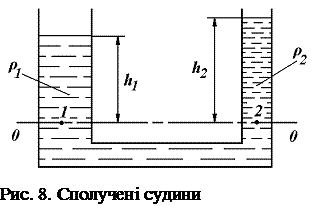На рис. 1.8 приведена схема сполучених судин, заповнених рідинами, що не змішуються, з різними  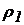і 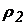 щільністю. Проведемо по границі розділу двох рідин у правому коліні площина рівного тиску, слід якої на схемі – горизонтальна лінія 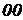. Абсолютні тиски в крапках  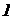і 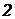, як і в будь-яких інших крапках рідини, що лежать на цій площині, будуть однакові: 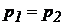. Відповідно до основного рівняння гідростатики (27)  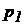і 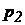 можуть бути замінені їх значеннями  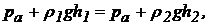відкіля

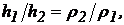                                                                                (1.31)

тобто висоти стовпів рідин у сполучених судинах назад пропорційні їх щільностям.

Якщо в сполучені посудини буде налита та сама рідина, то рівні її в обох колінах розташуються на однаковій висоті, тому що 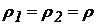 і, отже, з рівняння (31) 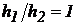, тобто .

 

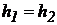Закон Паскаля

Помістимо на вільну поверхню рідини, що знаходиться в рівновазі в резервуарі (рис. 9, а), поршень і прикладемо до нього силу 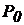, у результаті чого з боку поршня на рідину виникає тиск 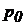. Відповідно до основного рівняння гідростатики (1.27) абсолютні тиски в довільно обраних крапках рідини 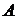, , 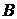 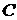будуть відповідно рівні:

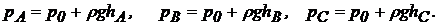
З аналізу отриманих рівнянь видно, що абсолютні тиски в крапках рідини, що знаходяться на різній глибині, будуть різні, однак зовнішній тиск на рідину, укладену в замкнутій судині, передається всім її часткам без зміни. У цьому суть закону Паскаля.

Практично закон Паскаля використовується в ряді гідравлічних машин: гідравлічних пресах і підйомниках, об'ємних насосах і гідродвигунах.

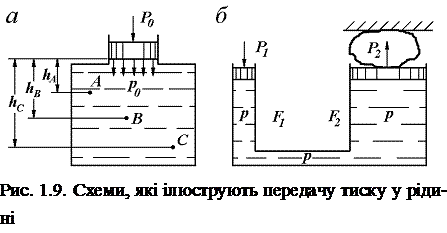На рис. 9, б приведена принципова схема гідравлічного преса. Прикладаючи до меншого поршня силу 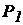, створюємо в рідині тиск 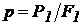, що відповідно до закону Паскаля передається більшому поршню, викликаючи силу 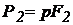. Якщо зневажити опорами, то

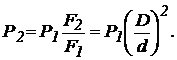                                                                       (32)