Диференціальні рівняння рівноваги рідини

Виділимо навколо крапки 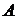, що знаходиться усередині спочиваючої рідини, елементарний об'єм у виді паралелепіпеда (рис. 4) з ребрами 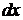, , 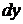, 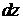рівнобіжними довільно обраним у просторі осями координат. Відкинемо думкою навколо паралелепіпеда рідину, замінивши її дію на грані відповідними силами гідростатичного тиску.

Нехай тиск рідини в крапці 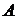 дорівнює 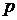, тоді тиск на грані  буде: на ліву , на праву , де  – збільшення тиску уздовж осі  на відстані .

Елементарні сили тиску на грані  будуть відповідно рівні:

та

Аналогічним чином можна знайти елементарні сили, що діють на інші чотири грані (на рис. 4 показані тільки тиски, що діють на осі ).

Крім поверхневих сил на виділений обсяг діють також масові сили, результуюча яких в загальному випадку буде

Спроектуємо всі діючі на елементарний обсяг сили на вісь  і дорівняємо суму цих проекцій нулю:

чи

Після приведення подібних і скорочення доданків, що залишилися,  на одержимо. Спроектувавши інші сили на осі  і 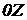, і зробивши аналогічні перетворення, одержимо систему рівнянь:

, , ,                                   (24)

з яких видно, що збільшення гідростатичного тиску в напрямку якої-небудь координатної осі можливо тільки при наявності прискорення в цьому напрямку і відбувається за рахунок масових сил. Ці рівняння являють собою загальні умови рівноваги рідини в диференціальній формі, виведені в 1755 р. Л.Ейлером.

Для приведення рівнянь Ейлера до виду, зручному для інтегрування, помножимо кожне з рівнянь (1.24) відповідно на 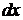, , 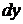 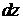і складемо почленно:

У цьому рівнянні ліва частина є повним диференціалом тиску , то

                                                                    (25)

Отримане рівняння виражає функціональну залежність тиску від роду рідини і координат крапки в просторі і дозволяє визначити значення тиску в будь-якій крапці рідини, що знаходиться в рівновазі. Це рівняння справедливе для краплинних рідин і для газів, причому для газів додатковою умовою рівноваги є рівняння стану (4).

З вираження (25) можна легко одержати рівняння поверхні рівного тиску – поверхні, тиск у всіх крапках якого однаково ().

При , а тому що , отже,

                                                                            (26)

Рівняння (26) – рівняння поверхні рівного тиску, окремим випадком якої є вільна поверхня рідини. Розглянемо кілька конкретних прикладів і установимо, який вид буде мати поверхня рівного тиску (у тому числі і вільна поверхня) у цих випадках.

Випадок 1. Рідина знаходиться в рівновазі в резервуарі в поле дії тільки сили ваги (рис. 5, а). У цьому випадку проекції результуючої одиничних масових сил будуть: 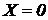, , 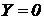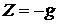. Підставляючи ці значення в (26), одержимо  чи після інтегрування .

Це – рівняння горизонтальної площини. Отже, у спочиваючій однорідній рідині (  ) будь-яка горизонтальна площина є площиною рівного тиску.

Випадок 2. Рідина знаходиться в рівновазі в резервуарі, що рухається горизонтально з деяким прискоренням 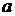 (рис. 5, б). У цьому випадку будь-яка частка рідини знаходиться під дією прискорень  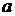і , отже, проекції результуючої одиничних масових сил будуть: , , . Підставляючи ці значення в (26), одержимо  чи після інтегрування .

Це – рівняння похилої площини. Отже, у даному випадку поверхні рівного тиску являють собою площини, нахилені до осей  і 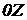 і рівнобіжні осі . Кут нахилу площини до обрію може бути знайдений з вираження .

Випадок 3. Рідина знаходиться в рівновазі в циліндричному резервуарі, що обертається навколо вертикальної осі з постійною кутовою швидкістю  (рис. 5, в). У цьому випадку будь-яка частка рідини знаходиться під дією прискорень  і відцентрової сили інерції , отже, проекції результуючої одиничних масових сил будуть: , , . Підставляючи ці значення в (1.26), одержимо  чи після інтегрування , але тому що , то .

Це – рівняння параболоїда обертання. Отже, у даному випадку поверхні рівного тиску являють собою сімейство параболоїдів обертання навколо вертикальної осі. При перетині їхньою вертикальною площиною вийде сімейство парабол з вершиною на осі 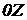, а при перетині горизонтальною площиною – сімейство концентричних окружностей з центром на осі .

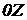В останніх двох прикладах розглянуті випадки так називаного відносного спокою рідини, коли вона знаходиться в резервуарах, що рухаються тим чи іншим способом з постійним прискоренням, але частки рідини не переміщаються друг щодо друга і щодо стінок резервуара.