2018-02-14
1548
Соединения бывают: 1. По прямым; 2. По каналам (жгутовые соединения) ® отдельные проводники собирают в жгут и образуют канал
При трассировке рассматривается совокупность эквипотенциальных контактов, нужно определить, как их соединить.
Если контакты - вершины в графе, то решение задачи трассировки - дерево с минимальной суммарной длиной (весом) ребер.
Алгоритм Прима:
1. Выбирается произвольная вершина и соединяется с ближайшей (кратчайшим путём). Получается фрагмент из двух элементов.
2. Выбирается вершина, ближайшая к фрагменту (то есть минимальное расстояние от любой вершины, входящей в фрагмент, до любой, еще не включенной в него). Эта вершина добавляется во фрагмент.
3. Повторять пункт 2 пока есть вершины, не принадлежащие фрагменту.
Граф удобно представить в виде матрицы соединений.
Полный граф – граф, в котором каждая вершина соединена с каждой, т.е. вершины попарно смежные. Граф имеет 
связей.
Пример: Имеется 5 контактов, заданы длины проводов.
1) Строим полный граф и вычисляем расстояния для каждого элемента.
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 0 | 6 | 5 | 4 | 6 |
| 2 | 6 | 0 | 8 | 10 | 8 |
| 3 | 5 | 8 | 0 | 6 | 11 |
| 4 | 4 | 10 | 6 | 0 | 7 |
| 5 | 6 | 8 | 11 | 7 | 0 |
| верш. | длина |
| 4 – 1 | 4 |
| 1 – 3 | 5 |
| 1 – 2 | 6 |
| 1 – 5 | 6 |
| L= | 21 |
k = nn-2; k – кол-во возможных деревьев; n – кол-во вершин
Задача соед. с min длиной – построение min дерева – min покрываюшее\связывающее
2) Берем произв. вершину. Пусть = 4
3) Ищем в строке 4 верш. с min значением (верш. 1 – значение 4). Соединяем 4 и 1
4) В строках фрагмента (1 и 4) ищем min число (верш. 3 – значение 5). Соед. 1 и 3
5) Повтор. п.4 для полученного фрагмента
18. Алгоритм трассировки проводных соединений с ограничением проводников на один контакт.
Модифицированный алгоритм Прима учитывает максимальное количество соединений для элемента. То есть даже если элемент ближайший, но у него исчерпан лимит соединений- он не будет соединён, а соединён будет следующий ближайший.
1. Выбирается произвольная вершина и соединяется с ближайшей Þ фрагмент из двух эл-тов.
2. Выбирается вершина, ближайшая к фрагменту с учетом ограничения (т.е. min расстояние от любой вершины, входящей в фрагмент, не считая тех, у которых кол-во соединений уже равно max возможному, до любой, еще не включенной в него) и добавляется во фрагмент.
3. Повторять пункт 2 пока есть вершины, не принадлежащие фрагменту.
1)Строим полный граф и вычисляем расстояние для каждого элемента:
| 1 | 2 | 3 | 4 | 5 | ||
| 1 | 0 | 6 | 5 | 4 | 6 | k=1+1=max |
| 2 | 6 | 0 | 8 | 10 | 8 | |
| 3 | 5 | 8 | 0 | 6 | 11 | k=1 |
| 4 | 4 | 10 | 6 | 0 | 7 | k=1+1=max |
| 5 | 6 | 8 | 11 | 7 | 0 | k=1 |
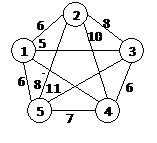
| верш. | длина |
| 5 – 1 | 6 |
| 1 – 4 | 4 |
| 4 – 3 | 6 |
| 3 – 2 | 8 |
1) Пусть max k =2. Берем произв. верш. (пусть – 5). Лок. степ. k(5):= 1
2) Ищем в строке 5 верш. с min значением (верш. 1 – значение 6). k(1):= 1. Соед. 5 и 1.
3) Исключаем столбцы 1 и 5
4) Ищем в строках фрагмента, в к-ых лок. ст. < k (1 и 5) верш. с min значением (в строке 1 – верш. 4 –– значение 4). k(1) += 1 = max. k(4):=1. Соед. 1 и 4.
Если у строки k достигает ограничение – вычеркиваем. Вычерк. 1 строку ® 5) Повторяем п.4
Примеч.: в данном алг. увелич. Σ-ой длины проводников < 5% при кол. верш.=15
19. Алгоритм трассировки проводных соединений с заданными начальной и конечной точками.
1. Контакты - вершины в графе. Строим полный граф, рассчитав расстояния.
2. Составляется неубывающая последовательность длин всех ребер полного графа.
3. Для всех ребер из послед-сти: ребро добавляется, если выполняются следующие условия:
1) Оно не должно быть инцидентным начальной и конечной вершине
2) При включении очередного ребра, локальная степень вершины не должна превышать 2, а локальная степень начальной и конечной вершин - 1.
3) Включаемое ребро не должно образовывать цикл с уже включенными ребрами
4) При включении ребра, кроме последнего (n-1)-го, не должно существовать пути между начальной и конечной вершинами. Пример:
| верш. | длина | подходит |
| 1 – 4 | 4 | + |
| 1 – 3 | 5 | + |
| 1 – 2* | 6 | – |
| 1 – 5* | 6 | – |
| 3 – 4 | 6 | – |
| 4 – 5* | 7 | + |
| 2* – 3 | 8 | + |
| 2*–5* | 8 | |
| 2* – 4 | 10 | |
| 3 – 5* | 11 |
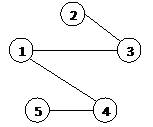
1) Построили полный граф. Вычислили длины проводников
2) Упорядочили по длине: (*-вершина конечная)
3) Þ соединили (1– 4) Þ соединили (1–3)
Þ (1–2), (1–5) нельзя из-за локальной степени;
Þ (3–4) нельзя – получается замкнутая цепь;
Þсоединили (4–5) Þ соединили (2–3)
20. Эвристический алгоритм построения дерева Штейнера.
Этапы трассировки многослойных печатных плат:
1. [Что?] Для каждой цепи (подмножества эквипотенциальных контактов) определяется порядок соединения этих контактов
2. [Где?] Определение кол-ва слоев полупроводников и распределение проводников по слоям
3. [Когда?] В каком порядке проводить соединения
4. [Как?] Выполнение собственно трассировки
Рассмотрим 1-й этап: определение порядка соединения контактов. Используется алгоритм Прима, который не зависит от метрики, но при построении дерева Штейнера, которое от метрики зависит принципиально, используются ортогональные соединения, и необходимо задуматься о том, как можно минимизировать длину проводников.
Теорема: пусть есть совокупность эквипотенциальных контактов. Построим ортогональную сетку путем испускания ортогональных проводников до пересечения друг с другом. Соединение контакт-проводник, проводник-проводник могут иметь место лишь в узлах данной решетки.
Алгоритм: 1. Находим по Приму минимальное остовное (покрывающее) дерево.
2. Рассмотрим пару вершин с минимальным расстоянием и соединим их проводником.
3. Для всех оставшихся вершин: при рассмотрении очередной вершины следующий фрагмент проводника формируется так, чтобы обеспечить максимальное совмещение с уже проложенными проводниками. При равенстве выбирается любой.
| Пары: (1-2) (2-5) (5-4) (5-6) (4-3) (6-7) (6-8) |
Пример: Допустим в результате алгоритма Прима получили след. послед. пар контактов:
Соединяем контакты ортогональными прямыми в этом же порядке. После того как провели (1-2) есть 2 варианта провести (2-5):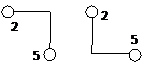 
Выбираем по принципу сопоставления 2 вариант.
21. Точный алгоритм построения дерева Штейнера.
Имеем ортогональную сетку. Граф G = (V, E), где V - узлы сети, включая заданные, а вес ребра - ортогональное (Манхэттенское) расстояние между узлами решетки. Каждому ребру сопоставим булеву переменную x1,..., xk. Тогда каждому пути S на графе можно сопоставить конъюнкцию булевых переменных. Ks = x1∧...∧xr (большая буква К означает конъюнкцию).
Пусть т. h - верхний левый угол ортогональной сетки, а т. k - нижний правый угол ортогональной сетки. Тогда все множество путей можно описать как дизъюнкию конъюнкций всех возможных путей. fh,k = ∨Ks, s ∈ Mh,k, где Mh,k - множество путей.
Рассмотрим множество путей между двумя соседними вершинами (пусть эти две вершины имеют индексы i и i+1). fi,i+1 = ∨Ks, s ∈ Mi,i+1 ® F(P1,..., Pn) = ∧fi,i+1, где i = 1,..., n-1
Приводим эту функцию к ДНФ, и в полученном выражении выделяем конъюнктивные члены, среди них ищем конъюнкцию наименьшей длины (т.е. с наименьшим кол-вом букв). Буквы данной конъюнкции отвечают ребрам ортогональной сетки, по которым необходимо провести проводник. Но это не обязательно будет оптимальным решением. Чтобы найти оптимальное решение, надо найти конъюнкцию соответствующую наименьшему пути, а длина пути вычисляется как сумма весов ребер. Поэтому как правило чем меньше ребер (букв в конъюнкции), тем короче путь.
