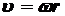СПРАВОЧНИК ПО ОСНОВНЫМ РАЗДЕЛАМ ФИЗИКИ ДЛЯ ПОДГОТОВКИ СТУДЕНТОВ К ИНТЕРНЕТ- ЭКЗАМЕНУ.
I. МЕХАНИКА.
Кинематика.
| Поступательное движение | Вращательное движение |
Путь S = 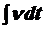 ;
Скорость v = dS/dt;
Ускорение a = dv/dt; ;
Скорость v = dS/dt;
Ускорение a = dv/dt;
| Угол j = 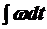 ;
угловая скорость w = dj /dt;
угловое ускорение ε = dw /dt ;
угловая скорость w = dj /dt;
угловое ускорение ε = dw /dt
|
| Связь между параметрами поступательного и вращательного движения | |
Равномерное поступательное движение:
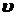 = const; a = 0; S = = const; a = 0; S = 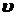 t t
| Равномерное вращательное движение: w = const; ε = 0; j = wt |
Равноускоренное движение: a = const ¹ 0;
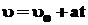 ; S = ; S = 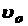 t + at2/2; t + at2/2;
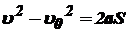
| Равноускоренное движение: ε = const ¹ 0;
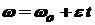 ; ; 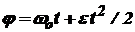
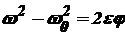
|
Тело, брошенное под углом a к горизонту со скоростью nо.
Движение вдоль оси ОX: 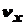 = const; x =
= const; x = 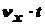 = (nо. cos a) ×t;
= (nо. cos a) ×t;
и ОY: 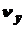 = nо. sin a - gt; y =
= nо. sin a - gt; y = 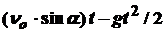
В верхней точке траектории: 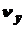 = nо. sin a - gtо = 0;
= nо. sin a - gtо = 0;
Время движения tо до верхней точки траектории: tо = nо. sin a/ g
Время движения тела до падения: t = 2 tо = 2 nо. sin a / g
Дальность полета вдоль оси ОX до падения: S = 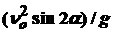
Максимальная высота подъема тела: H = 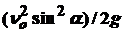
Движение по окружности.
Тангенциальное (касательное) ускорение 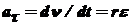 .
.
Центростремительное (нормальное) ускорение 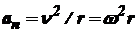 .
.
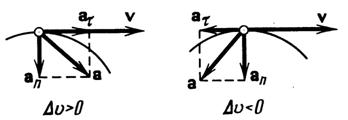 Модуль вектора полного ускорения
Модуль вектора полного ускорения 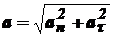 .
.
Динамика
| 1. Поступательное движение | 2. Вращательное движение |
Сила 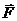
| Момент силы 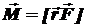 , где , где 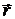 радиус-вектор – вектор от оси вращения в точку приложения силы радиус-вектор – вектор от оси вращения в точку приложения силы
|
Импульс 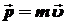
| Момент импульса 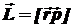
|
| Масса тела m | Момент инерции тела J = 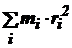
|
Основное уравнение динамики
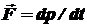 , , 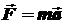
| Основное уравнение динамики
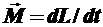 , , 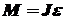
|
Работа 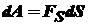
| Работа 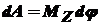
|
Кинетическая энергия 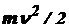
| Кинетическая энергия 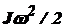
|
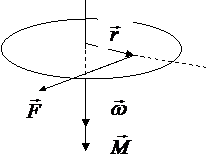
3.Направление момента силы M и момента импульса L находится по правилу правого винта (смотри пример на рисунке).
Моменты инерции некоторых тел простейшей формы
| Тело | Положение оси | Момент инерции |
| Полый тонкостенный цилиндр радиусом R | Ось симметрии | 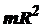
|
| Сплошной цилиндр или диск радиусом R | Ось симметрии | 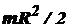
|
|
Тонкий прямой стержень длиной l | Ось перпендикулярна стержню и проходит через его середину | 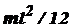
|
| Ось перпендикулярна стержню и проходит через его конец | 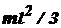
| |
| Шар радиусом R | Ось проходит через центр шара | (2/5) 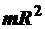
|
| Теорема Штейнера: I= Io + ma2, где a – расстояние между осями. | ||
4.Уравнение динамики материальной точки массой m в неинерциальной К′ системе отсчета, вращающейся с постоянной угловой скоростью w вокруг неподвижной оси: m a′ = F + mw2 r + 2m [ 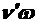 ]
]
5.Уравнение динамики тела переменной массы (уравнение Мещерского):
m a = F + u dm/dt, где u- скорость отделения вещества относительно тела.
6.Уравнение динамики системы тел идентично уравнению движения материальной точки, вся масса которой сосредоточена в центре масс, к которому приложены и все действующие силы. Радиус-вектор R центра масс системы тел c общей массой m: R = 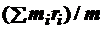 . Если радиус-векторы тел
. Если радиус-векторы тел 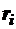 откладывать от центра масс системы, то R = 0 и
откладывать от центра масс системы, то R = 0 и 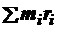 =0.
=0.
7. Связь между силой и потенциальной энергией U частицы в поле: F = - 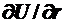
Движение планет и комет
1. Уравнение движения планеты массой m1 вокруг звезды массой m2 под действием гравитационной силы: m1 dv/dt = - (G m1 m2 / r3) 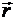 .
.
2. Сила, действующая на движущуюся вокруг звезды планету, направлена вдоль радиус-вектора планеты, поэтому момент этой силы равен 0: M = [r F] = 0.
Т.к. M = dL/dt=0, то при движении планеты вокруг звезды момент ее импульса не меняется как по модулю, так и по направлению: L=[rmv]=mr2(dj/dt)=const.
3. Первая космическая скорость 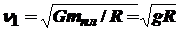 - скорость, при которой тело может стать спутником планеты массой
- скорость, при которой тело может стать спутником планеты массой 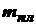 и радиусом R. Находится из равенства гравитационной Gm
и радиусом R. Находится из равенства гравитационной Gm 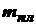 /R2 и центростремительной
/R2 и центростремительной 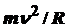 сил. Для Земли
сил. Для Земли 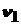 =7,9 км/сек.
=7,9 км/сек.
Вторая космическая скорость 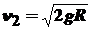 =
= 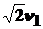 - скорость, при которой тело может преодолеть гравитационное притяжение планеты. Находится из равенства кинетической и потенциальной энергии тела.
- скорость, при которой тело может преодолеть гравитационное притяжение планеты. Находится из равенства кинетической и потенциальной энергии тела.
Законы Кеплера:
1. Каждая планета движется по эллипсу, в фокусе которого находится Солнце.
2. Радиус-вектор планеты за равные промежутки времени Dt описывает одинаковые площади величиной DS = (L/2m) Dt, где m - масса планеты, L - ее момент импульса. 3. Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит.
 2018-02-14
2018-02-14 680
680
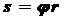 ;
;