Электромагнитные волны

1.Плотность потока энергии электромагнитной волны 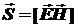 - вектор Пойтинга.

2. Скорость распространения электромагнитных волн в среде 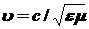, ε – электрическая, μ – магнитная проницаемость среды, с – скорость света.

3. Объемная плотность энергии электромагнитного поля W = ED/2 + BH/2

4. Импульс электромагнитного поля , W – энергия поля.

 

МОЛЕКУЛЯРНАЯ (СТАТИСТИЧЕСКАЯ) ФИЗИКА и ТЕРМОДИНАМИКА

Идеальные газы

1. Давление р идеального газа на стенку сосуда: р = n kT = , 

  Т - температура, n – концентрация,  - скорость, m –масса молекул газа.

2. Уравнение состояния идеального газа p = nkT

 Уравнение Клайперона – Менделеева: ,

     m –масса газа, М - молярная масса, n - число молей; V - объем газа.

Молярной массой М вещества называется масса его 1 моля, а 1 моль вещества численно равен относительной молекулярной массе  его молекул, выраженной в граммах: = .

Молярные массы некоторых газов.

газ	относительная молекулярная масса  (безразмерная величина)	Молярная масса М
Водород - H2	2
Гелий - He	4
Аргон - Ar	40
Кислород - O2	32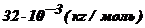
Азот - N2	28
Углекислый газ  - CO2	44
Вода - H2O	18

 Смеси идеальных газов.

1. В смеси идеальных газов для каждого i-ого газа можно записать уравнение Клайперона – Менделеева .  

Величина  в данном уравнении называется парциальным давлением.

2. Давление смеси газов на стенки сосуда равно сумме парциальных давлений компонент смеси: P =  - закон Дальтона.

3.Уравнение Клапейрона-Менделеева для смеси газов:

                          

где - эффективная молярная масса смеси газов.

      = =

где 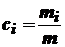 - массовая концентрация; а  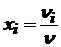- молярная концентрация i-ого газа в смеси,  - суммарное число молей в смеси газов.

Функции распределения Максвелла:

1. j ()  = ; dN/N = dP =j ()d -

 относительное число молекул, скорость  которых лежит в интервале [ ; + d ] и вероятность dP этого явления.

2. f()= ; dN/N= dP =f() d - относительное число молекул и вероятность того, что компоненты ,  и  их скоростей меняются в интервалах: [ ; + d ]; [ ; + d ];[ ; + d ].

3. F()= ; dN/N = dP = F()d -

относительное число молекул, модули скоростей которых лежат в интервале [ ; + d ] и вероятность этого явления.

---

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:  

---

123