Релятивистская механика

1. Релятивистское замедление часов: =  - интервал времени , измеренный движущимися часами, меньше времени  неподвижных часов. 

2. Релятивистское сокращение длины =  - длина движущегося тела   вдоль направления движения меньше, чем длина  неподвижного тела.

3. Преобразования Лоренца:

x′ = (x-n t)/ ; y′ = y; z′ = z;      t′ = (t - xn /c²)/ .

Обратные преобразования: x = (x′+n t′) / ;

t = (t′ - x′n / c²)/    где x′; y′; z′; t′- координаты и время в системе К ′, движущейся со скоростью n относительно системы К, причем оси x и x′ совпадают, а оси y и z параллельны.

4. Связь между скоростями тела в системе К и движущейся со скоростью V вдоль оси X системы К ′: = ; = ; =  

4.Масса релятивистской частицы:   m = m_o / .

4. Релятивистский импульс = / , где m_o - масса покоя.

6. Полная энергия релятивистской частицы

                                 = / =

КОЛЕБАНИЯ И ВОЛНЫ.

2.2.1. Механические колебания

Тип колебаний	Уравнение	его решение	Амплитуда А и частота w
Собственные гармонические колебания			А=Aо=const; wo – частота собственных колебаний
Затухающие гармонические колебания	b - коэффициент затухания	= t - время релаксации  -логарифмический декремент затухания; Q =  -  добротность колебательной системы
Вынужденные колебания	= = fo cos(w t+j)	, где wравна частоте изменения силыF= m× fo	А=  Резонанс амплитуды (максимум А) на частоте:

 

Круговая (циклическая) частота w (рад/сек) , Т – период (сек),

ν – частота (Гц).

Скорость 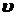и ускорение a смещения точек при гармонических колебаниях:

          .

.

Сложение колебаний.

Результирующее колебание из нескольких колебаний одинаковой частоты находится с помощью векторной диаграммы, на которой каждое из колебаний представляется в виде вектора, длина которого равна амплитуде колебания, а угол с осью OX  равен фазе колебания. Согласно рис. 2.1, результатом сложения двух гармонических колебаний равной частоты

  X₁ = A₁ cos (wt + j₁) и X₂ = A₂ cos (wt + j₂)

является колебание X = A cos (wt + j), с фазой tg j =  и амплитудой А = .

Примеры гармонических осцилляторов:

Маятник	Уравнение движения	Собственная частота	Период колебания Т
Пружинный; - упругая сила	или k –жесткость пружины
Физический	, α – угол отклонения тела	= = J- момент инерции тела	- приведенная длина маятника
Математи- ческий

2.2.2. Электрические колебания

Затухающие колебания в электрическом колебательном контуре (рис. 2.2) описываются уравнением , b = R/2L; w = ; w_o=1/ ; период колебаний Т=2 p/ w; л огарифмический декремент затухания ; добротность Q = . При малом затухании Q = w_oL / R.

Вынужденные колебания. При подключении колебательного контура к источнику переменного напряжения U=U_o coswt в нем возникают вынужденные колебания тока I = I_о cos (wt - j)  с амплитудой I_о= U_o /  и фазой tgj = (wL - 1/wC)/R.  Максимум I_о наблюдается на частоте w_o=1/ . На данной частоте напряжение на емкостном R_c=1/wC и индуктивном сопротивлении  оказывается одинаковым, но сдвинутым по фазе на p ( рис. 2.3). Поэтому ток в контуре определяется только активным сопротивлением R - резонанс напряжений.

2.2.3. Волны

1. Уравнение плоской (бегущей) волны ,

или по формуле Эйлера , где k - волновое число,

w - частота колебаний, - смещение   частиц.

2. Уравнение сферической волны (волновые поверхности имеют вид концентрических сфер) .

3. Скорость перемещения волны – есть скорость перемещения постоянной фазы, т.е. . Дифференцируя это уравнение по времени, находим скорость перемещения волны: u = dx/dt = w / k.

4. Длина волны = 2p / k, где T=2p /w - период колебаний частиц в волне

5. Волновое уравнение: .

6. Стоячие волны возникают  при наложении двух бегущих волн  и   одинаковой амплитуды и частоты, двигающихся навстречу друг другу:

= + = + = (2Acoskx) sinwt =B sinwt

В результате наложения таких волн в каждой точке среды возникает гармоническое колебание той же частоты w, но с амплитудой B = 2A coskx, зависящей от координаты x. Когда B = max - пучности, B =min – узлы. В пространстве шириной d могут возникнуть стоячие волны такой длины волны l, при которой в нем укладывается целое число N полуволн: d =N∙ l/2.