Методика применения метода наименьших квадратов предполагает, что значения случайной переменной попарно не коррелированы, или они попарно независимы в вероятностном смысле. Если же переменные содержат тренд или циклические колебания, то последовательные остатки могут быть коррелированы. Такой вид корреляции называется автокорреляцией остатков или возмущений.
Автокорреляция остатков затрудняет применение классических методов анализа временных рядов. В моделях регрессии, которые описывают зависимости между случайными значениями взаимозависимых величин, она снижает эффективность применения МНК.
Для определения автокорреляции остатков используют критерий Дарбина-Уотсона.
Пример 3.
Провести проверку параболической функции, построенной в примере 1, на наличие автокорреляции остатков.
Решение.
Параболическая функция, которая построена в примере 1, имеет вид: 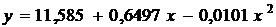 .
.
Для проверки ее на наличие автокорреляции с помощью критерия Дарбина-Уотсона рассчитывается d-статистика по формуле (7):
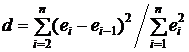 , (7)
, (7)
где 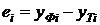 ,
, 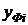 – фактические значения показателя,
– фактические значения показателя, 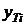 – соответствующие теоретические значения показателя.
– соответствующие теоретические значения показателя.
Для того, чтобы рассчитать d-статистику построим вспомогательную таблицу:
Таблица 6 - Расчет d-статистики
| и | 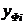 | 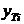 | 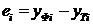 | 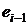 | 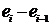 | 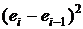 | 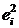 |
| 1 | 12,1 | 12,2251 | -0,1251 | 0,01565 | |||
| 2 | 12,9 | 12,8445 | 0,0555 | -0,1251 | 0,1806 | 0,032616 | 0,00308 |
| 3 | 13,7 | 13,4437 | 0,2563 | 0,0555 | 0,2008 | 0,040321 | 0,06569 |
| 4 | 13,9 | 14,0227 | -0,1227 | 0,2563 | -0,379 | 0,143641 | 0,015055 |
| 5 | 14,5 | 14,5815 | -0,0815 | -0,1227 | 0,0412 | 0,001697 | 0,006642 |
| 6 | 15,1 | 15,1201 | -0,0201 | -0,0815 | 0,0614 | 0,00377 | 0,000404 |
| 7 | 15,7 | 15,6385 | 0,0615 | -0,0201 | 0,0816 | 0,006659 | 0,003782 |
| 8 | 16,1 | 16,1367 | -0,0367 | 0,0615 | -0,0982 | 0,009643 | 0,001347 |
| 9 | 16,6 | 16,6147 | -0,0147 | -0,0367 | 0,022 | 0,000484 | 0,000216 |
| 10 | 17,1 | 17,0725 | 0,0275 | -0,0147 | 0,0422 | 0,001781 | 0,000756 |
 | 0,240612 | 0,112623 |
С помощью формулы (7) рассчитываем d – статистику:
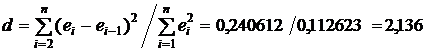
Вычисленное значение d сравнивается с интервалами, найденными в соответствии со значениями 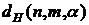 и
и 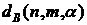 (приложение 2). Здесь п – количество наблюдений, т – число факторов,
(приложение 2). Здесь п – количество наблюдений, т – число факторов, 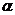 – уровень значимости. В нашем случае критические значения статистики Дарбина-Уотсона при 5%-ном уровне значимости, то есть при
– уровень значимости. В нашем случае критические значения статистики Дарбина-Уотсона при 5%-ном уровне значимости, то есть при 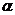 =0,05, равняются:
=0,05, равняются: 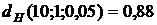 и
и 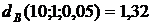 .
.
Таблица 7 – Расчет интервалов
| Принимаем гипотезу о существовании положительной автокорреляции | Зона неопре-делен-ности | Принимаем гипотезу об отсутствии автокорреляции | Зона неопре-делен-ности | Принимаем гипотезу о существовании отрицательной автокорреляции |
0 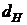 | 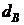 2 2 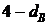 | 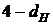 4 4 | ||
| 0 0,88 | 1,32 2 2,68 | 3,12 4 |
Из таблицы 7 видим, что d - статистика удовлетворяет неравенству:
1,32 < 2,136 < 2,68,
значит принимаем гипотезу об отсутствии автокорреляции остатков.
Замечание. Если значение d-статистики удовлетворяет неравенствам 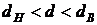 или
или 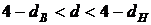 , то при выбранном уровне значимости не возможно сделать вывод о наличии или об отсутствии автокорреляции остатков, необходимо дальнейшее исследование.
, то при выбранном уровне значимости не возможно сделать вывод о наличии или об отсутствии автокорреляции остатков, необходимо дальнейшее исследование.
На практике при количественной оценке параметров эконометрической модели довольно часто сталкиваются с проблемой взаимосвязи между объясняющими переменными. Если взаимосвязь довольно тесная, то оценка параметров модели может иметь большую погрешность. Такая взаимосвязь между объясняющими переменными называется мультиколлинеарностью. Мультиколлинеарность переменных приводит к смещению оценок параметров модели. Поэтому необходима проверка факторов на мультиколлинеарность.
Наиболее простой формой проверки мультиколлинеарности является анализ корреляционной матрицы. Значение парных коэффициентов корреляции свидетельствует о том, связаны между собою переменные или нет. Но если в модели большее двух факторов, вопрос о мультиколлинеарности не может ограничиваться информацией, которая дает эта матрица. Более общая проверка предусматривает вычисление определителя матрицы R, (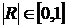 ).
).
Наиболее полное исследование мультиколлинеарности можно осуществить на основе алгоритма Феррара-Глаубера. Этот алгоритм включает три вида статистических критериев, на основе которых проверяется мультиколлинеарность всего массива переменных (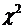 , хи-квадрат); каждой факторной переменной со всеми другими (F-статистика) и мультиколлинеарность каждой пары факторов (t-статистика). Все эти критерии при сравнении с их критическими значениями дают возможность сделать конкретные выводы относительно наличия или отсутствия мультиколлинеарности независимых переменных.
, хи-квадрат); каждой факторной переменной со всеми другими (F-статистика) и мультиколлинеарность каждой пары факторов (t-статистика). Все эти критерии при сравнении с их критическими значениями дают возможность сделать конкретные выводы относительно наличия или отсутствия мультиколлинеарности независимых переменных.
Пример 4.
Затратына питание зависят от факторов:общие затраты, состав семьи и заработок. Надо исследовать наличие мультиколлинеарностипо алгоритму Феррара-Глаубера.
Затраты на питание, 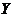 | Общие затраты, 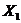 | Состав семьи, 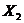 | Заработок, 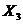 |
| 22 | 45 | 1,7 | 70 |
| 30 | 72 | 1,9 | 105 |
| 45 | 131 | 2 | 172 |
| 62 | 228 | 3,4 | 302 |
| 48 | 90 | 3 | 150 |
| 64 | 145 | 3,6 | 205 |
| 76 | 225 | 4,7 | 303 |
| 108 | 357 | 5,2 | 480 |
| 65 | 136 | 4,9 | 195 |
| 90 | 218 | 5 | 315 |
Решение.
1. Найдем корреляционную матрицу. Эта матрица симметричная. В нашем случае размера 3х3. Она имеет вид:
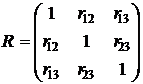 , (8)
, (8)
где 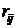 исчисляется по формуле
исчисляется по формуле
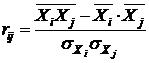 , (9)
, (9)
где 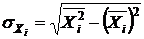 ,
, 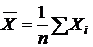 ,
, 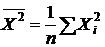 .
.
Вычислим вспомогательную таблицу:
Таблица 8 - Расчет элементов корреляционной матрицы
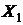 | 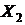 | 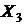 | 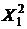 | 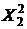 | 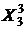 | 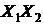 | 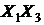 | 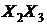 |
| 45 | 1,7 | 70 | 2025 | 2,89 | 4900 | 76,5 | 3150 | 119 |
| 72 | 1,9 | 105 | 5184 | 3,61 | 11025 | 136,8 | 7560 | 199,5 |
| 131 | 2 | 172 | 17161 | 4 | 29584 | 262 | 22532 | 344 |
| 228 | 3,4 | 302 | 51984 | 11,56 | 91204 | 775,2 | 68856 | 1026,8 |
| 90 | 3 | 150 | 8100 | 9 | 22500 | 270 | 13500 | 450 |
| 145 | 3,6 | 205 | 21025 | 12,96 | 42025 | 522 | 29725 | 738 |
| 225 | 4,7 | 303 | 50625 | 22,09 | 91809 | 1057,5 | 68175 | 1424,1 |
| 357 | 5,2 | 480 | 127449 | 27,04 | 230400 | 1856,4 | 171360 | 2496 |
| 136 | 4,9 | 195 | 18496 | 24,01 | 38025 | 666,4 | 26520 | 955,5 |
| 218 | 5 | 315 | 47524 | 25 | 99225 | 1090 | 68670 | 1575 |
| 1647 | 35,4 | 2297 | 349573 | 142,16 | 660697 | 6712,8 | 480048 | 9327,9 |
В нашем случае число испытаний 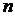 равняется 10. Из таблицы 8 имеем:
равняется 10. Из таблицы 8 имеем:
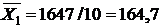 | 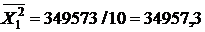 | 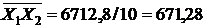 |
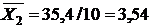 | 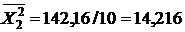 | 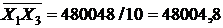 |
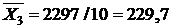 | 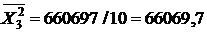 | 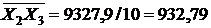 |
Рассчитаем средние квадратичные отклонения:
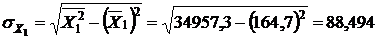
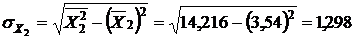

Рассчитанные значения подставим в формулу (9):
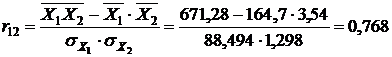
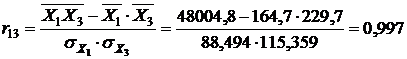
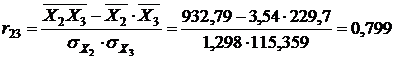
Для данной задачи корреляционная матрица (8) имеет вид:
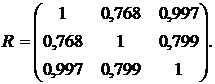
Элементы этой матрицы характеризуют тесноту связи между факторами.
В нашем случае 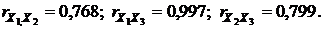 Между каждой парой факторов существует определенная связь.
Между каждой парой факторов существует определенная связь.
2. Найдем определитель 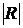 корреляционной матрицы
корреляционной матрицы 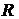 по формуле (10):
по формуле (10):
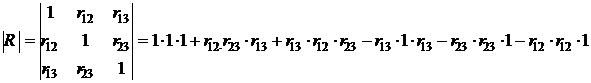 (10)
(10)
В нашем случае получим такие результаты:
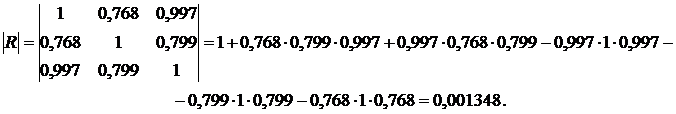 Найдем
Найдем 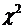 - статистику по формуле (11):
- статистику по формуле (11):
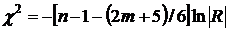 (11)
(11)
В нашем случае число испытаний 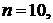 число факторов
число факторов 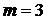 , поэтому формула (11), имеет вид:
, поэтому формула (11), имеет вид: 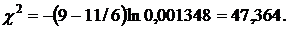
При степени свободы 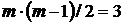 и уровне значимости
и уровне значимости 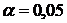 находим по таблице (приложение 3) критическое значение
находим по таблице (приложение 3) критическое значение 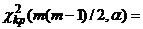
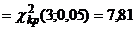 .
.
Если 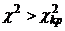 , то мультиколлинеарность существует, в противном случае, то есть при
, то мультиколлинеарность существует, в противном случае, то есть при 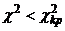 мультиколлинеарность отсутствует.
мультиколлинеарность отсутствует.
В нашем случае поскольку 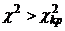 (
(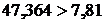 ), то можем считать что мультиколлинеарность присутствует.
), то можем считать что мультиколлинеарность присутствует.
3. Найдем обратную матрицу 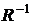 к матрице
к матрице 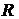 с помощью формулы (12)
с помощью формулы (12)


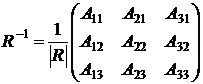 , (12)
, (12)
где 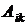 – алгебраическое дополнение к элементу
– алгебраическое дополнение к элементу 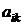 .
.
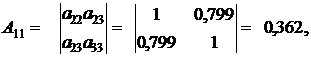 | 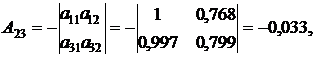 |
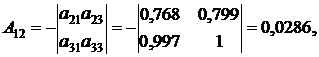 | 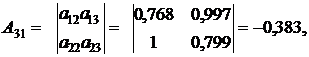 |
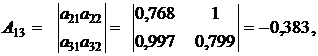 | 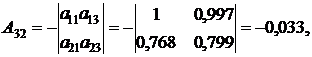 |
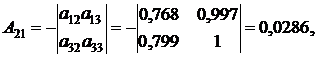 | 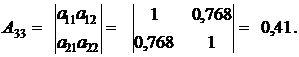 |
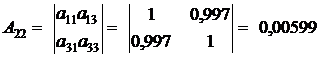 |
Найденные алгебраические дополнения подставим в формулу (12):
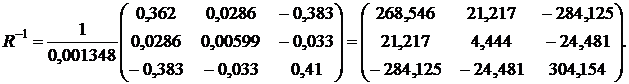
4. Рассчитаем 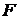 - статистику по формуле (13):
- статистику по формуле (13):
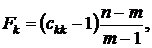 (13)
(13)
где 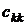 – диагональные элементы матрицы
– диагональные элементы матрицы 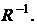
В нашем случае 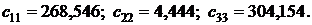 Эти значения подставим в формулу (13). Получим
Эти значения подставим в формулу (13). Получим
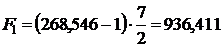 ;
; 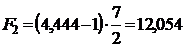 ;
; 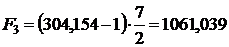
Фактические значения статистики 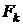 сравниваются с табличными
сравниваются с табличными 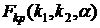 (приложение 4) при
(приложение 4) при 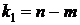 и
и 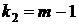 степенях свободы и уровне значимости
степенях свободы и уровне значимости 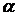 . Если
. Если 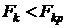 , то переменная
, то переменная 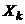 с другими не коррелирует. В противоположном случае, то есть если
с другими не коррелирует. В противоположном случае, то есть если 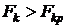 , то переменная
, то переменная 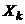 коррелирует с другими переменными.
коррелирует с другими переменными.
В нашем случае при уровне значимости 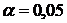 и степенях свободы
и степенях свободы 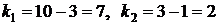 табличное значение критерия равняется
табличное значение критерия равняется 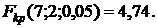 Поскольку все
Поскольку все 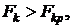 то можно сделать вывод, что переменные коррелируют между собой.
то можно сделать вывод, что переменные коррелируют между собой.
5. Найдем частные коэффициенты корреляции.
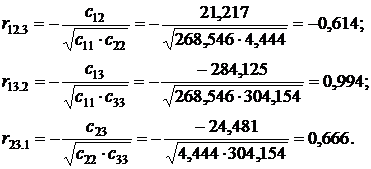
Частные коэффициенты корреляции характеризуют тесноту связи между двумя переменными при условии, что третья не влияет на эту связь.
Частный коэффициент 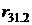 приблизительно равен парному. Это свидетельствует о наличии мультиколлинеарности между переменными
приблизительно равен парному. Это свидетельствует о наличии мультиколлинеарности между переменными 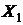 и
и 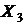 .
.
6. Рассчитаем значения 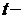 статистик:
статистик:
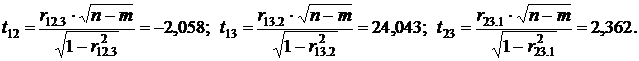
Табличное значение 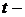 статистики при 7 степенях свободы и уровне значимости 0,05 (приложение 5) равняется
статистики при 7 степенях свободы и уровне значимости 0,05 (приложение 5) равняется 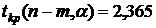 . Если
. Если 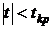 , то между соответствующими переменными нет мультиколлинеарности. В противоположном случае, то есть если
, то между соответствующими переменными нет мультиколлинеарности. В противоположном случае, то есть если 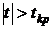 , между соответствующими переменными имеется существенная мультиколлинеарность.
, между соответствующими переменными имеется существенная мультиколлинеарность.
Найденное фактическое значение 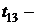 критерия больше табличного значения. Можно сделать вывод, что между переменными
критерия больше табличного значения. Можно сделать вывод, что между переменными 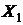 и
и 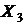 также возможна коллинеарность. Сравнивая эти результаты, можем заключить, что из рассмотрения следует исключить фактор
также возможна коллинеарность. Сравнивая эти результаты, можем заключить, что из рассмотрения следует исключить фактор 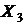 .
.
4 МНОЖЕСТВЕННАЯ РЕГРЕССИЯ
Каждое явление в природе, экономике, общественной жизни, технике определяется комплексом причин. На уровень развития одного показателя могут влиять много факторов. Уровень влияния факторов на показатель может существенно различаться. Все эти закономерности следует учитывать во время проведения эконометрического анализа, прогнозирования и планирования.
При существовании линейной зависимости объясняемой переменной (показателя) 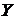 от нескольких объясняющих переменных (факторов)
от нескольких объясняющих переменных (факторов) 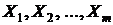 общее выражение уравнения множественной регрессии имеет вид (14):
общее выражение уравнения множественной регрессии имеет вид (14):
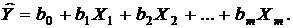 (14)
(14)
Модель описывает совместное одновременное влияние факторов на показатель. Задача исследования состоит в оценке параметров регрессии 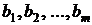 по результатам выборочных наблюдений над переменными, которые включены в модель. Построение модели проводят методом наименьших квадратов.
по результатам выборочных наблюдений над переменными, которые включены в модель. Построение модели проводят методом наименьших квадратов.
Пример 5.
Построить эконометрическую модель, которая характеризует зависимость между затратами на питание 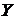 (условные денежные единицы), общими затратами
(условные денежные единицы), общими затратами 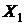 (условные денежные единицы) и составом семьи
(условные денежные единицы) и составом семьи 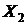 (количество членов семьи) на основе данных, которые приведенные в таблицы.
(количество членов семьи) на основе данных, которые приведенные в таблицы.
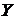 | 22 | 30 | 45 | 62 | 48 | 64 | 76 | 108 | 65 | 90 |
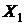 | 45 | 72 | 131 | 228 | 90 | 145 | 225 | 357 | 136 | 218 |
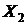 | 1,7 | 1,9 | 2 | 3,4 | 3 | 3,6 | 4,7 | 5,2 | 4,9 | 5 |
Решение. Для построения линейной многофакторной модели (15)
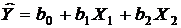 , (15)
, (15)
где 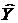 – теоретические значения показателя.
– теоретические значения показателя.
В соответствии с методом наименьших квадратов параметры 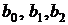 ищут как решение системы линейных уравнений (16)
ищут как решение системы линейных уравнений (16)
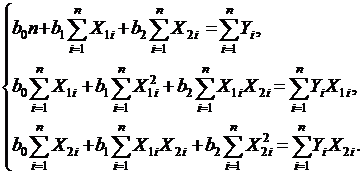 (16)
(16)
Вспомогательные вычисления удобно проводить в таблице:
Таблица 9 - Расчет элементов системы (16)
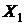 | 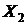 | 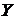 | 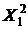 | 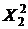 | 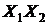 | 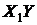 | 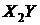 |
| 45 | 1,7 | 22 | 2025 | 2,89 | 76,5 | 990 | 37,4 |
| 72 | 1,9 | 30 | 5184 | 3,61 | 136,8 | 2160 | 57 |
| 131 | 2 | 45 | 17161 | 4 | 262 | 5895 | 90 |
| 228 | 3,4 | 62 | 51984 | 11,56 | 775,2 | 14136 | 210,8 |
| 90 | 3 | 48 | 8100 | 9 | 270 | 4320 | 144 |
| 145 | 3,6 | 64 | 21025 | 12,96 | 522 | 9280 | 230,4 |
| 225 | 4,7 | 76 | 50625 | 22,09 | 1057,5 | 17100 | 357,2 |
| 357 | 5,2 | 108 | 127449 | 27,04 | 1856,4 | 38556 | 561,6 |
| 136 | 4,9 | 65 | 18496 | 24,01 | 666,4 | 8840 | 318,5 |
| 218 | 5 | 90 | 47524 | 25 | 1090 | 19620 | 450 |
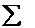 1647 1647 | 35,4 | 610 | 349573 | 142,16 | 6712,8 | 120897 | 2456,9 |
В последней строке записывают суммы чисел в столбце. Можно найти средние для каждого показателя по формулам (17)-(19)
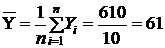 ; (17)
; (17)
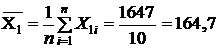 ; (18)
; (18)
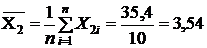 . (19)
. (19)
Система (16) для определения параметров регрессии имеет вид:
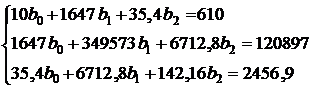
Из первого уравнения можно выразить 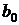 и подставить во второе и третье уравнения:
и подставить во второе и третье уравнения:
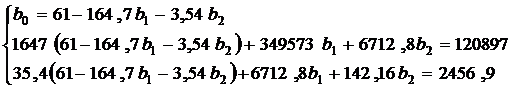
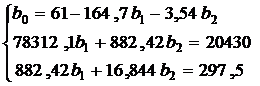
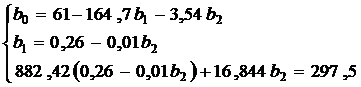
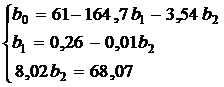
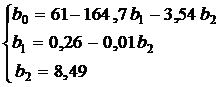
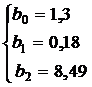
Тогда уравнение регрессии (15) имеет вид
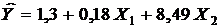 . (20)
. (20)
Важным этапом регрессионного анализа является оценка практической значимости синтезированной модели. Проверку значимости модели проводят на основании показателей тесноты связи между признаками 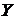 и
и 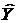 .
.
Множественный коэффициент корреляции 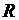 равен коэффициенту корреляции между фактическими и теоретическими значениями объясняемой переменной. Его вычисляют по формуле (21)
равен коэффициенту корреляции между фактическими и теоретическими значениями объясняемой переменной. Его вычисляют по формуле (21)
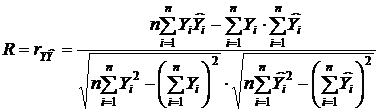 (21)
(21)
Для вычисления множественного коэффициента корреляции целесообразно рассчитать вспомогательную таблицу:
Таблица 10 - Расчет элементов коэффициента 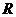
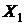 | 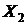 | 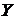 | 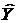 | 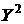 | 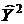 | 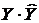 |
| 45 | 1,7 | 22 | 23,83 | 484 | 568,01 | 524,33 |
| 72 | 1,9 | 30 | 30,39 | 900 | 923,61 | 911,73 |
| 131 | 2 | 45 | 41,86 | 2025 | 1752,26 | 1883,70 |
| 228 | 3,4 | 62 | 71,21 | 3844 | 5070,29 | 4414,77 |
| 90 | 3 | 48 | 42,97 | 2304 | 1846,42 | 2062,56 |
| 145 | 3,6 | 64 | 57,96 | 4096 | 3359,83 | 3709,70 |
| 225 | 4,7 | 76 | 81,70 | 5776 | 6675,38 | 6209,43 |
| 357 | 5,2 | 108 | 109,71 | 11664 | 12035,85 | 11848,46 |
| 136 | 4,9 | 65 | 67,38 | 4225 | 4540,20 | 4379,77 |
| 218 | 5 | 90 | 82,99 | 8100 | 6887,34 | 7469,10 |
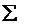 610 610 | 610,01 | 43418 | 43659,19 | 43413,54 |
В соответствии с формулой (21) множественный коэффициент корреляции равняется
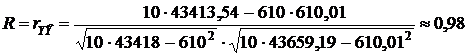 .
.
Чем более близок 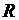 к единице, тем лучше данная модель описывает фактические данные. Рассчитанный коэффициент указывает на очень точное соответствие математической модели фактическим данным.
к единице, тем лучше данная модель описывает фактические данные. Рассчитанный коэффициент указывает на очень точное соответствие математической модели фактическим данным.
Коэффициент детерминации 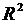 равен квадрату множественного коэффициента корреляции. Он измеряет долю общей дисперсии относительно среднего
равен квадрату множественного коэффициента корреляции. Он измеряет долю общей дисперсии относительно среднего 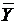 , которую можно объяснить регрессией.
, которую можно объяснить регрессией.
В нашем случае 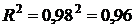 . То есть 96% дисперсии показателя
. То есть 96% дисперсии показателя 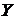 (затраты на питание) можно объяснить с помощью построенной модели зависимости от
(затраты на питание) можно объяснить с помощью построенной модели зависимости от 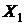 (общих затрат) и
(общих затрат) и 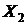 (состава семьи).
(состава семьи).
Полезным является построение интервальных границ для коэффициента множественной регрессии.
Интервал доверия для множественного коэффициента корреляции находится по формуле (22)
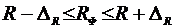 , (22)
, (22)
где 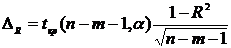 .
.
В нашем случае по таблицам Стьюдента (приложение 5) находим критическую точку 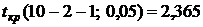 , поэтому
, поэтому 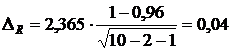 .
.
Тогда доверительный интервал, найденный по формуле (22), имеет вид 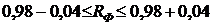 или
или 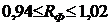 . Поскольку коэффициент множественной корреляции должен находиться в границах от 0 до 1, то доверительным интервалом для него будет
. Поскольку коэффициент множественной корреляции должен находиться в границах от 0 до 1, то доверительным интервалом для него будет 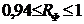 , что указывает на очень точный подбор модели.
, что указывает на очень точный подбор модели.
Проверку значимости уравнение регрессии делают таким образом: по критерию Фишера вычисляют фактическое значение 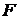 -статистики (23):
-статистики (23):
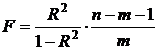 . (23)
. (23)
По таблице критических точек Фишера (приложение 4) находят критическое значение статистики 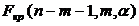 , где
, где 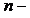 количество наблюдений,
количество наблюдений, 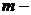 количество факторов,
количество факторов, 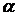 – уровень значимости.
– уровень значимости.
Если 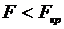 , то уравнение регрессии не является значимым, коэффициент множественной корреляции
, то уравнение регрессии не является значимым, коэффициент множественной корреляции 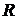 не существенно отличается от нуля. Если
не существенно отличается от нуля. Если 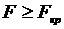 , то уравнение регрессии является значимым, коэффициент множественной корреляции
, то уравнение регрессии является значимым, коэффициент множественной корреляции 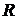 существенно отличается от нуля.
существенно отличается от нуля.
В нашем случае рассчитаем 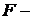 статистику по формуле (23)
статистику по формуле (23) 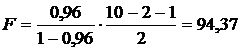 . По таблицам Фишера (приложение 4) найдем критическое значение
. По таблицам Фишера (приложение 4) найдем критическое значение 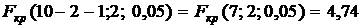 . Поскольку
. Поскольку 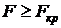 , то уравнения считают значимым.
, то уравнения считают значимым.
Экономический смысл параметра bi регрессии: если фактор 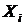 изменится на единицу своего измерения, то показатель
изменится на единицу своего измерения, то показатель 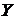 изменится на
изменится на 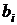 единиц своего измерения при условии, что остальные факторы остаются без изменений.
единиц своего измерения при условии, что остальные факторы остаются без изменений.
В нашем случае 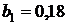 . Если фактор
. Если фактор 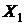 изменится на единицу своего измерения, то показатель
изменится на единицу своего измерения, то показатель 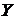 изменится на
изменится на 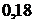 единиц своего измерения. То есть если общие затраты возрастут (или уменьшатся) на 1 условную денежную единицу, то затраты на питание возрастут (или уменьшатся) на
единиц своего измерения. То есть если общие затраты возрастут (или уменьшатся) на 1 условную денежную единицу, то затраты на питание возрастут (или уменьшатся) на 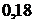 условных денежных единиц. Поскольку
условных денежных единиц. Поскольку 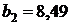 , то если фактор
, то если фактор 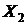 изменится на 1 единицу своего измерения, то показатель
изменится на 1 единицу своего измерения, то показатель 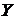 изменится на
изменится на 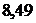 единиц своего измерения. То есть если количество членов семьи возрастет (или уменьшится) на одного человека, то затраты на питание возрастут (или уменьшатся) на
единиц своего измерения. То есть если количество членов семьи возрастет (или уменьшится) на одного человека, то затраты на питание возрастут (или уменьшатся) на 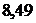 условных денежных единиц.
условных денежных единиц.
 2018-02-14
2018-02-14 1330
1330
