Выяснение тесноты связи между у и х

Ход работы

Имеются следующие исходные данные:

Таблица 1

Исходные данные

Y	X
4,37	1,08
4,01	1,53
3,29	2,05
3,1	2,58
3,22	3,02
2,99	3,58
2,9	4,06
2,37	4,56
1,87	5,01
1,82	5,51
1,89	6,06
2,28	6,52
1,46	7,02
1,56	7,53
1,73	8,05
	8,48

Где 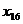 - прогнозное значение фактора x.

Исходные данные формируются в первых двух столбцах A3:A17, C3:C17. Блок промежуточный данных – D3:U17. Прогнозные значения вычисляются в 18 ряде.

Для нахождения средних значений столбцов отводим 21 ряд. Используем встроенную функцию СРЗНАЧ.

Для нахождения сумм столбцов отводим 24 ряд и используем встроенную функцию СУММ.

Нахождение оценок параметров

Вводится гипотеза, что между фактором X и показателем Y существует следующая стохастическая зависимость: 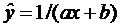. Заменой Y1=  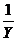приводим нелинейную парную регрессию к парной линейной .

 

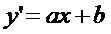Параметры модели вычисляются по формулам:

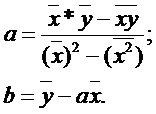
Значение параметра а находится в ячейке В26. Формула имеет вид =(B21*A21-D21)/(B21^2-E21)

a= 0,06;

Значение параметра b находится в ячейке В27. Формула имеет вид =A21-B21*B26

b= 0,16

Также найдем оценки параметров с помощью функции ЛИНЕЙН(B3:B17;C3:C17;1;1) в диапазоне ячеек A40:B44.

Таблица 2

Результат работы функции ЛИНЕЙН

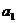
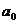
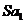
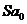
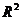
	S
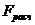
	Степени  свободы
SST	SSE

Таблица 3

Результат работы функции ЛИНЕЙН для данной задачи

 

0,060479	0,156676
0,006999	0,035182
0,851731	0,058277
74,67854	13
0,253625	0,044151

 

Расчет теоретических значений У

Рассчитываем теоретические значения У по формуле 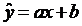в ячейках G3:G17. В ячейку F3 вводим формулу =$B$26*B3+$B$27.

Т.к. имеющаяся функция является обратной к линейной, то для нахождения ее теоретического значения в ячейку G3 вводим формулу =1/F3.

Для прогнозного значения х₁₆= 8,48 найдем значение y по формуле у_р= .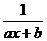

у_р= 1,49.

 

Выяснение тесноты связи между у и х

Для выяснения тесноты связи можно воспользоваться двумя методами:

-построение точечной диаграммы:

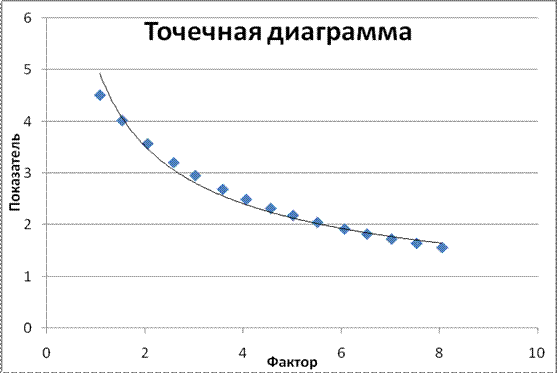
Рис.1 – Точечная диаграмма

- использование коэффициента корреляции r

(-1<=r<=1)

Для нахождения коэффициента корреляции можно воспользоваться следующими формулами:

- Встроенная функция Excel КОРРЕЛ(B3:B17;C3:C17);

r₁= 0,92

- Линейный коэффициент корреляции:

а)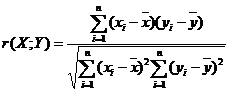

r₂= 0,92

б)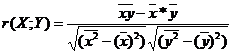

r₃= 0,92

Так как коэффициент корреляции при вычислении всеми тремя способами равен r=0,92, то между у и х наблюдается тесная линейная связь.

Индекс корреляции:

Индекс корреляции вычисляется по следующей формуле:

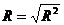
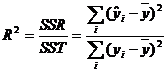
Значение коэффициента детерминации находится в ячейке В46.

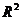=0,85

Индекс корреляции R=0,92 находится в ячейке B47.Для парной линейной регрессии R²=r², следовательно R=r=0,92