Множественная корреляция

Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, или оценивает тесноту совместного влияния факторов на результат.

Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции:

                                            

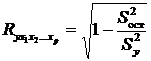
где S ²_ост – остаточная сумма квадратов для уравнения y = f (x ₁, x ₂,…, x_p); S ² _y – общая сумма квадратов результативного признака.

Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов.

Можно пользоваться следующей формулой индекса множественной корреляции

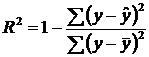.                                                   (3.7)

                                          (3.8)

Формула индекса множественной корреляции для линейной регрессии получила название линейного коэффициента множественной корреляции или совокупного коэффициента корреляции.

Найдем для нашего примера совокупный коэффициент корреляции:

.

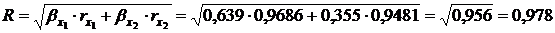Для того чтобы не допустить возможного преувеличения тесноты связи, применяется скорректированный индекс (коэффициент) множественной корреляции

Скорректированный индекс множественной корреляции содержит поправку на число степеней свободы, а именно остаточная сумма квадратов 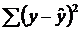 делится на число степеней свободы остаточной вариации (п – т – 1), а общая сумма квадратов отклонений  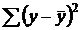– на число степеней свободы в целом по совокупности (п – 1).

Формула скорректированного индекса множественной детерминации имеет вид:

,                             (3.17)

где п – число наблюдений; т – число параметров при переменных

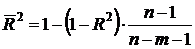.                                       (3.18)

Чем больше величина т, тем сильнее различия 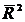  и R 2.

Для линейной зависимости признаков скорректированный коэффициент множественной корреляции определяется по той же формуле, что и индекс множественной корреляции, Т.е. как корень квадратный из 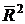. Отличие состоит лишь в том, что в линейной зависимости под т подразумевается число факторов, включенных в регрессионную модель, а в криволинейной зависимости т – число параметров при х и их преобразованиях (x ², ln х и др.), которое может быть больше числа факторов как экономических переменных.

ЧАСТНАЯ КОРРЕЛЯЦИЯ

Частные коэффициенты (или индексы) корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии.

Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель.

Предположим, что зависимость y x ₁ характеризуется уравнением

y_{x 1} = a + b ₁ × x ₁.

Подставив в это уравнение фактическое значение x ₁, найдем теоретические величины 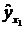 и соответствующую величину остаточной дисперсии s ²:

.

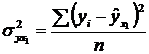Включив в уравнение регрессии дополнительный фактор x ₂, получим уравнение регрессии вида

y_{x 1 x 2} = a + b ₁ × x ₁ + b ₂ × x ₂.

Чем большее число факторов включено в модель, тем меньше величина остаточной дисперсии, т.е. происходит ее сокращение. Чем больше доля этого сокращения в остаточной вариации до введения дополнительного фактора, тем теснее связь между y и x ₂ при постоянном действии фактора x ₁. Следовательно, чистое влияние фактора x ₂ на результат y можно найти как

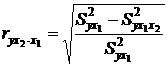.                                              (3.19)

Знак «точка» в выражении частного коэффициента корреляции r_{yx 2× x 1} означает элиминирование той переменной (переменных), которая стоит после знака «точка».

Аналогично определяется и чистое влияние на результат y фактора x ₁:

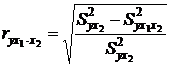.                                              (3.20)

Если выразить остаточную дисперсию через показатель детерминации S ²_ост = S ² _y (1 – r ²), то формула коэффициента частной корреляции примет вид:

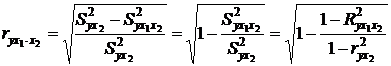.                          (3.21)

Соответственно

.                                                  

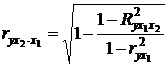Рассмотренные показатели частной корреляции принято называть коэффициентами (индексами) частной корреляции первого порядка, ибо они фиксируют тесноту связи двух переменных при закреплении (элиминировании влияния) одного фактора.

Если рассматривается регрессия с числом факторов р, то возможны частные коэффициенты корреляции не только первого, но и второго, третьего,..., (р – 1) порядка, т. е. влияние фактора x ₁ можно оценить при разных условиях независимости действия других факторов:

r_{yx 1× x 2} – при постоянном действии фактора x ²;

r_{yx 1× x 2 x 3} – при постоянном действии факторов x ² и x ³;

r_{yx 1× x 2… xp} – при неизменном действии всех факторов, включенных в уравнение регрессии.

Сопоставление коэффициентов частной корреляции разных порядков по мере увеличения числа включаемых факторов показывает процесс «очищения» связи результативного признака с исследуемым фактором.

Хотя частная корреляция разных порядков и может представлять аналитический интерес, в практических исследованиях предпочтение отдают показателям частной корреляции самого высокого порядка, ибо именно эти показатели являются дополнением к уравнению множественной регрессии.

В общем виде при наличии р факторов для уравнения

y = a + b ₁ × x ₁ + b ₂ × x ₂ + … + b_p × x_p + e.

коэффициент частной корреляции, измеряющий влияние на у фактора x_i; при неизменном уровне других факторов, можно определить по формуле

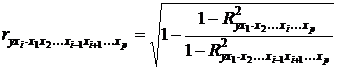.                           (3.23)

где 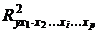 – множественный коэффициент детерминации всего комплекса р факторов с результатом;  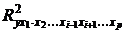– тот же показатель детерминации, но без введения в модель фактора x_i.

При i = 1 формула коэффициента частной корреляции примет вид:

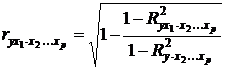.                                            (3.24)

Данный коэффициент частной корреляции позволяет измерить тесноту связи между у и x_i при неизменном уровне всех других факторов, включенных в уравнение регрессии.

Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается. Например, r_{yx 1× x 2} – коэффициент частной корреляции первого порядка. Соответственно коэффициенты парной корреляции называются коэффициентами нулевого порядка. Коэффициенты частной корреляции более высоких порядков можно найти через коэффициенты частной корреляции более низких порядков по рекуррентной формуле

.                  (3.25)

При двух факторах и i = 1 данная формула примет вид:

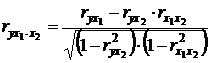.                                               (3.26)

Соответственно при i = 2 и двух факторах частный коэффициент корреляции у с фактором x ₂ можно определить по формуле

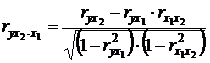.                                               (3.27)

 

В основном их используют на стадии формирования модели, в частности в процедуре отсева факторов.

Зная частные коэффициенты корреляции (последовательно первого, второго и более высокого порядка), можно определить совокупный коэффициент корреляции по формуле

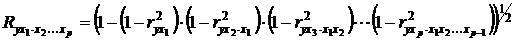.      (3.31)

При полной зависимости результативного признака от исследуемых факторов коэффициент совокупного влияния их равен единице. Из единицы вычитается доля остаточной вариации признак (1 – r ²), обусловленная последовательно включенными в анализ факторами. В результате подкоренное выражение характеризует совокупное действие всех исследуемых факторов.

№15

Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью F -критерия Фишера:

                                                  

где s ²_факт – факторная дисперсия на одну степень свободы; R ² – коэффициент (индекс) множественной детерминации; n – число наблюдений; m – число параметров при переменных x (в линейной регрессии совпадает с числом включенных в модель факторов); s ²_ост – остаточная дисперсия на одну степень свободы.

Определяем все суммы квадратов и дисперсии. Общая сумма квадратов:

.

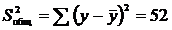Остаточная сумма квадратов:

.

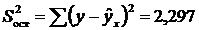Факторная:

.

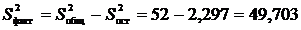Факторная дисперсия на одну степень свободы

.

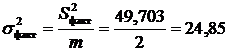Остаточная дисперсия на одну степень свободы s ²_ост и вытекающую из нее стандартную ошибку s:

             .

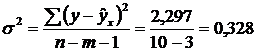
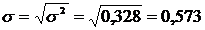Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F -отношения, т.е. критерий F:

.

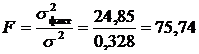Или по формуле (3.32):

.

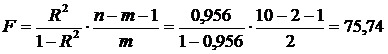Оценивается значимость не только уравнения в целом, но и фактора, дополнительно включенного в регрессионную модель. Необходимость такой оценки связана с тем, что не каждый фактор, вошедший в модель, может существенно увеличивать долю объясненной вариации результативного признака. Кроме того, при наличии в модели нескольких факторов они могут вводиться в модель в разной последовательности. Ввиду корреляции между факторами значимость одного и то го же фактора может быть разной в зависимости от последовательности введения в модель. Мерой для оценки включения фактора в модель служит частный F -критерий, т.е. F_xi.

С помощью частного F -критерия можно проверить значимость всех коэффициентов регрессии в предположении, что каждый соответствующий фактор x_i был введен в уравнение множественной регрессии последним.

Для проверки значимости коэффициентов регрессии определяется средняя квадратическая ошибка каждого коэффициента регрессии по формуле:

.

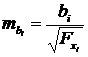Затем определяется значение t -критерия Стьюдента по известной формуле:

.

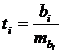Если величина частного F -критерия выше табличного значения, то это означает одновременно не только значимость рассматриваемого коэффициента регрессии, но и значимость частного коэффициента корреляции. Существует взаимосвязь между квадратом частного коэффициента корреляции и частным F -критерием, а именно

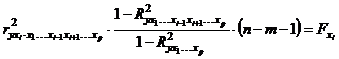,               (3.41)

где r ² _{yxi × x 1… xi –1 xi +1… xp} – частный коэффициент детерминации фактора x_i с y при неизменном уровне всех других факторов; 1 – R ² _{yx 1… xi –1 xi +1… xp} – доля остаточной вариации уравнения регрессии, включающего все факторы, кроме фактора x_i; 1 – R ² _{yx 1… xp} – доля остаточной вариации для уравнения регрессии с полным набором факторов.

Взаимосвязь показателей частного коэффициента корреляции, частного F -критерия и t -критерия Стьюдента для коэффициентов чистой регрессии может использоваться в процедуре отбора факторов. Отбор факторов при построении уравнения регрессии методом исключения практически можно осуществлять не только по частным коэффициентам корреляции, исключая на каждом шаге фактор с наименьшим незначимым значением частного коэффициента корреляции, но и по величинам t_bi и F_xi. Частный F -критерий широко используется и при построении модели методом включения переменных и шаговым регрессионным методом.

 

№16

нелинейному уравнению множественной регрессии, в качестве которого выбираем полный полином второго порядка:

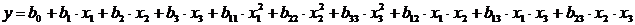
Для определения коэффициентов такого уравнения средствами Excel необходимо дополнительно сформировать 6 столбцов для расчета коэффициентов от b ₁₁ до b ₂₃. После этого применяем процедуру Регрессия \ Анализ данных. Результаты в следующей таблице:

Расчетные значения по этому уравнению приведены в соответствующем столбце таблицы. Статистические характеристики. Общая сумма квадратов:

.

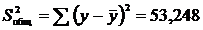Остаточная сумма квадратов:

.

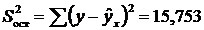Факторная:

.

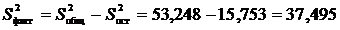Факторная дисперсия на одну степень свободы s _факт = 37,495/9 = 4,166. Остаточная дисперсия на одну степень свободы s ²_ост и вытекающая из нее стандартная ошибка s _ост:

                   .

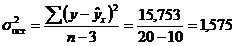
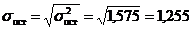Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F -отношения, т.е. критерий F:

.

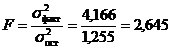Индекс множественной корреляции:

.

Коэффициент детерминации:

.

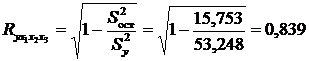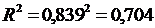Критерий Фишера по формуле (3.32):

.

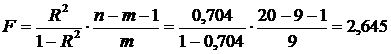Величина скорректированного индекса детерминации

.

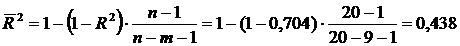Средняя ошибка аппроксимации A = (17,62 / 20) × 100 = 88,11 %. Или:

.

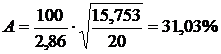Для полученных уравнений 1-го и 2-го порядков можно подсчитать все статистические характеристики, как в примере для линейной множественной регрессии: частный F -критерий, ошибки в определении коэффициентов и значения критериев Стьюдента для каждого из них, уравнение регрессии в стандартизованном масштабе и его статистические характеристики.