2018-02-14
6525
Магнетик: – вещество, способное намагничиваться.
Вектор намагничивания: - Суммарный магнитный момент единицы объема вещества называют вектором намагничивания. 
где 
магнитный момент i-го атома (молекулы) из их общего числа, в объёме 
.В СИ намагниченность измеряется в А/м.
Напряженность магнитного поля:это векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности J.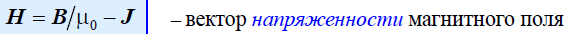 
, 
- магнитная постоянная.
Магнитная восприимчивость: - это физическая величина, характеризующая связь между магнитным моментом (намагниченностью) вещества и магнитным полем в этом веществе.
Магнитная проницаемость: - это физическая величина, характеризующая связь между магнитной индукцией 
и напряжённостью магнитного поля в веществеH.
С вязана с магнитной восприимчивостью χ следующим образом: в СИ: 
15. Теорема о циркуляции вектора H (в интегральной и дифференциальной формах). Поле в линейном однородном изотропном магнетике. Граничные условия на границе раздела двух магнетиков.
Теорема о циркуляции магнитного поля: - Циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающих контур циркуляции.
- интегр. форма 
- диффер. форма.
Поле в линейном однородном изотропном магнетике:
Граничные условия на границе раздела двух магнетиков:
Сосчитаем поток вектора B через поверхность малого
цилиндра, охватывающего границу раздела 2-х сред:
где S - площадь основания цилиндра, Sбок - площадь боковой
поверхности. Устремляя высоту цилиндра h 
0 и
S бок 
0, получаем на границе: 
и, учитывая, что 
и 
- противоположно направленные
нормали, и вводя общую нормаль n, имеем: 
Итак: нормальные составляющие вектора B непрерывны на границе раздела двух магнетиков.
Нормальные составляющие вектора H получим, используя соотношение 
Тогда из
имеем: 
Откуда получаем соотношение для нормальных составляющих напряженности магнитного поля:
