Волновая функция, ее интерпретация. Уравнение Шредингера. Стационарное уравнение Шредингера, его свойства

Волновая функция, или пси-функция 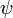- комплекснозначная функция, используемая в квантовой механике для описания чистого состояния системы.

Эта функция имеет вид Ψ(x. y, z, t).

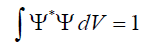Принимается, что волновые функции, отличающиеся только множителем, описывают одно и то же состояние. Это обстоятельство позволяет ввести условие нормировки на пси-функцию.

Вероятность dP обнаружения микрочастицы в пределах объема dV dP=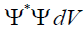

Постулируется принцип суперпозиции состояний. Если система может находиться в состояниях, описываемых волновыми функциями Ψ1, Ψ2, …, Ψ n, то она также может находиться в состоянии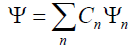

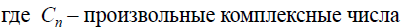
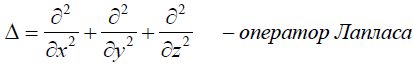Уравнение Шредингера: Общее временное уравнение Шредингера, позволяющее определить в любой момент времени волновую функцию  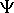для частицы массы 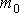, движущейся в силовом поле 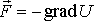, описываемом скалярной потенциальной функцией ,

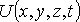имеет вид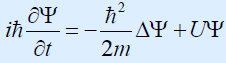

Стационарное уравнение Шредингера, его свойства:

имеет вид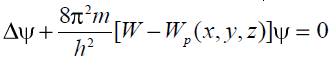

Уравнение справедливо для любой квантовой частицы движущейся со скоростью v < c и характеризуется следующими свойствами:

1) функция Ψ должна быть однозначной, непрерывной, конечной;

2) производные 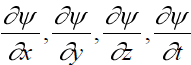 непрерывны;

3) функция |Ψ|²должна иметь конечный интеграл.