1. Абсолютна похибка прямих і непрямих вимірювань округляється до першого відмінного від “0” розряду (перша цифра зліва), тобто 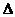 х записується з однією значущою цифрою.
х записується з однією значущою цифрою.
Наприклад: 
2. Середнє арифметичне значення вимірювання фізичної величини округляється до того самого розряду, що й абсолютна похибка вимірювання. Останній знак кінцевого результату повинен бути на такому розряді, на якому знаходиться перша значуща цифра його абсолютної похибки.
Наприклад: 

3. Відносна похибка вимірювань визначається з двома значущими цифрами.
Наприклад: 
4. В деяких випадках кінцевий результат доцільно записувати в нормалізованому вигляді:
 де n – порядок числа.
де n – порядок числа.
Наприклад: густина речовини 
§ 5-4. Використання довідкових таблиць.
А. Обчислення абсолютної похибки табличних величин.
Часто в робочу формулу, крім вимірюваних величин, входять фізичні величини, значення яких беруться з довідкових таблиць. Наприклад: прискорення вільного падіння, число π, густина, питома теплоємність, в’язкість і т.п.
Так як в числових значеннях величин, наведених у таблицях, залишені тільки вірні знаки, то абсолютна похибка табличних величин не може перевищувати половини одиниці останньої значущої цифри цього числа.
Наприклад: якщо прискорення вільного падіння g=9,81 м/с  , то
, то  м/с
м/с  ; π =3,14, то
; π =3,14, то 
Питома теплоємність міді С=395 Дж/кг К; 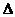 С=
С= 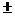 0,5 Дж/кг К.
0,5 Дж/кг К.
Густина води при 



У деяких таблицях дається залежність двох фізичних величин, одна з яких вимірюється безпосередньо. Наприклад, залежність густини води від температури, температури кипіння – від тиску і т.д. Абсолютна похибка такої величини зумовлена похибкою вимірювання аргументу. Наприклад, температура води 
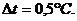 Необхідно визначити густину води і її абсолютну похибку
Необхідно визначити густину води і її абсолютну похибку  . Згідно таблиць маємо:
. Згідно таблиць маємо:
При 
 кг/м
кг/м 

 кг/м
кг/м 

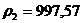 кг/м
кг/м 
Знаходимо середню швидкість зміни функції:
 кг/м
кг/м  К
К
Тоді абсолютна похибка приймає вигляд:
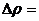 997,8
997,8 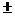 0,2 кг/м
0,2 кг/м  .
.
 2018-02-14
2018-02-14 214
214








