Метод логарифмічного диференціювання

Якщо розрахункова формула для визначення остаточного результату непрямих вимірювань є вираз, зручний для логарифмування, то в цьому випадку доцільно застосувати метод логарифмічного диференціювання (метод диференціювання натурального логарифма).

Нехай, розрахункова формула має вигляд:

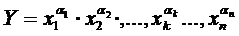
де 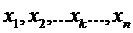 - будь – які раціональні числа. Тоді, проводячи логарифмування попереднього виразу, маємо:

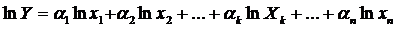
Після визначення повного диференціалу натурального логарифму одержимо:

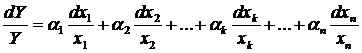
Замінюючи диференціали вимірюваних величин відповідними абсолютними похибками цих величин, одержаними при їх вимірюваннях, і взявши їх за модулем, дістанемо вираз для розрахунку максимальної відносної похибки:

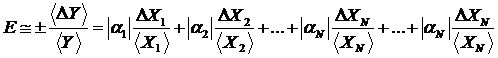
Більш точніший вираз отримаємо, переходячи до квадратичного додавання:

 

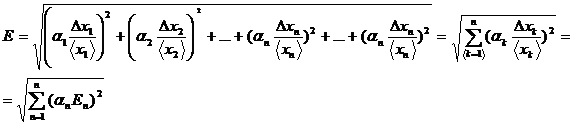
де 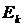 - відносні похибки окремих прямих вимірювань.

Приклад. Нехай розрахункова формула для обчислення густини твердого тіла циліндричної форми має вигляд:

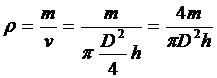
Проведемо логарифмування виразу:

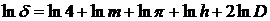
Визначимо повний диференціал натурального логарифму:

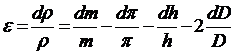
Замінюючи диференціал вимірюваних величин відповідними абсолютними похибками, знак “-” на знак “+”, одержимо формулу для абсолютного підрахунку максимальної відносної похибки:

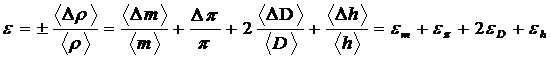
Квадратичне додавання приводить до виразу:

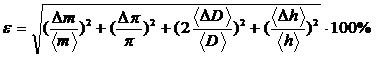
Максимальна абсолютна похибка визначається за формулою:

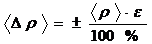
Кінцевий результат подаємо у вигляді:

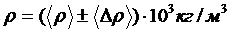
при р =0,95 і ε, %

Примітка: якщо шукана величина Y дорівнює сумі або різниці вимірюваних величин, то спочатку доцільно знайти абсолютну похибку, а потім – відносну.

Нехай,  ,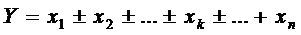

тоді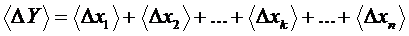

Квадратичне додавання дає формулу:

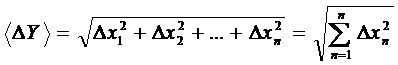
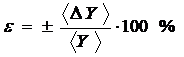
Математична обробка результатів фізичних вимірювань.