2018-02-12
266
Пример 1. ( Интегрирование с помощью замены переменной.)
Найти неопределенный интеграл 
.
Решение. Сделаем замену переменной 
, тогда 
Подставляя в подынтегральное выражение, получим
Пример 2. Найти интеграл 
.
Решение. Преобразуем подынтегральную функцию, выделив в числителе производную знаменателя. Для этого числитель представим в виде 
. Тогда
В первом интеграле сделаем замену переменной 
, 
. Получим
.
Для вычисления второго интеграла выделим в знаменателе полный квадрат 
.
Окончательно получим
Пример 3. (Интегрирование по частям). Найти неопределенный интеграл
I = 
x 2cos xdx
Решение. Полагаем u=x2; dv= cos xdx, v= sin x, du= 2 xdx.. В силу формулы интегрирования по частям udv=uv − vdu, имеем
I = х 2sin x − sin x 2 xdx.
Применяя к последнему интегралу еще раз формулу интегрирования по частям, получим (теперь уже u=x, dv= sin xdx)
I =x 2sin x − 2(−x cos x + cos xdx) = x2 sin x+2x cos x − 2sin x +C.
Замечание. В интегралах вида x m ln x dx; x m arctgx dx за функцию u(x) следует принимать ln x, arctg x соответственно.
|
|
|
Пример 4. (Интегрирование дробно-рациональной функции). Найти интеграл
I= 
.
Метод интегрирования дробно-рациональной функции заключается в разложении данной дроби на сумму многочлена и элементарных дробей и последующем интегрированием каждого слагаемого этого разложения. Рассмотрим эти два этапа решения на нашем примере.
Решение. 1). Подынтегральная функция имеет вид 
, где P (x) и Q(x) суть многочлены степени 5 и 4, соответственно:
P (x) =x 5 + 2 x 4 −x 2 + 3; Q (x)= (x− 1)2(x 2+1).
Однако прежде чем искать разложение дроби 
на сумму элементарных дробей, следует выделить из данной дроби целую часть (т.е. некоторый многочлен) и правильную дробь т.е. такую дробь, в которой степень числителя меньше степени знаменателя. С этой целью преобразуем знаменатель Q (x) = x 4 − 2 x 3+ 2 x 2 − 2 x + 1, после чего разделим многочлен P(x) на многочлен Q(x). Таким образом, получим
= x+ 4 + 
. (1)
Последняя дробь уже является правильной, поскольку степень числителя R(x)= 6x 3 − 7 x 2+7 x− 1 меньше степени знаменателя. Многочлен Q(x) имеет корень x= 1 кратности два, а также пару комплексно-сопряженных корней x=+i, x=−i поэтому разложение дроби R(x)/Q(x) следует искать в виде:
= 
, (2)
где числа А,В,С,D могут быть определены при помощи метода неопределенных коэффициентов. Приведем дроби, стоящие в правой части формулы (2), к общему знаменателю:
= 
, (3)
после чего приравняем числители в тождестве (3):
|
|
|
6 x 3 − 7 x 2+7 x− 1 = A (x 2+1)+ B (x− 1)(x 2+1)+(Cx+D) (x− 1)2.
Положив в тожестве (4) х =1, найдем А =5/2. Остальные коэффициенты разложения (2) можно определить, сравнивая коэффициенты при одинаковых степенях переменной х в левой и правой частях тождества (4). В результате такого сравнения получим систему линейных уравнений относительно неизвестных В, С, D следующего вида
х 3 В + С= 6
х 2 5/2 − В − 2 С +D =− 7
х 1 B+C − 2 D = 7
x 05/2 − B +D = − 1
Из этой системы последовательно находим D = − 1/2; В = 3; С = 3.
Таким образом, разложение (2) принимает вид:
= 
,
откуда, возвращаясь к формуле (1), получаем новое выражение для подынтегральной функции, а именно:
f (x)= x +4 + 
. (5)
2).После проделанных преобразований нахождение исходного интеграла сводится к нахождению суммы либо табличных интегралов, либо интегралов, легко приводящихся к табличным. Из формулы (5) последовательно получаем:
I= f(x)dx= xdx+ 4 dx+
+ 5/2 
= 
=
= 
(6)
Для нахождения последнего интеграла в формуле (6) проведем еще ряд несложных преобразований:
= 
− 
Oкончательно получаем
I= 
,
где С - произвольная постоянная.
Замечание 1. В случае, когда заданная подынтегральная функция представляет собой правильную дробь, производить деление числителя на знаменатель не нужно, а следует сразу переходить к разложению этой дроби на сумму элементарных дробей.
Замечание 2. При разложении правильной дроби на сумму элементарных дробей с помощью метода неопределенных коэффициентов необходимо иметь в виду следующее. Если многочлен, стоящий в знаменателе исходной дроби, имеет вещественный корень х0 кратности к 
1, то этому корню должна отвечать (в разложении на элементарные дроби) группа членов, состоящая в точности из к слагаемых следующего вида:
+ 
... + 
+ 
.
При этом не исключено, что после применения метода неопределенных коэффициентов какие-то из чисел Аi (i= 1,2,...,k) могут оказаться равными нулю.
Пример 5. (Интегрирование иррациональных функций). Найти интеграл
.
Решение. Легко видеть, что подстановка 
преобразует подынтегральное выражение к дробно-рациональному виду. В самом деле, если 
, то 2 x− 1= z 6, откуда dx= 3 z5dz, 
, 
. Поэтому
= 
.
Дальше можно применять уже известный метод интегрирования дробно-рациональных функций, однако в данном случае удобно применить следующий искусственный прием, который быстро приводит к цели:
= 
= 
=
=3 z − 3 arctg z+C = 3 
- 3 arctg 
+ C.
Пример 6. (Интегрирование тригонометрических функций). Найти интеграл
I= sin 2x cos 3xdx.
Решение. Выполним подстановку t= sin x, тогда dt= cos xdx, следовательно:
I= sin2 x cos 2x cos x dx= sin x (1 − sin2 x) cos xdx=
= t2 (1 − t2)dt = (t2−t4)dt=
=t3/ 3 − t5/ 5 + C =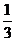 
sin 3x − 
sin 5 x +C.
Пример 7. Найти интеграл I = sin4 xdx.
Решение. Преобразуем подынтегральное выражение, применив формулу понижения порядка, известную из тригонометрии:
I= sin 4x dx= (sin2 x)2dx = 
(1 − cos2 x)2 dx=
= (1 − 2 cos2 x + cos 2 2 x) dx=
= (1 − 2cos2 x + (1+cos4 x)/2) dx =
= 
x− sin2 x + 
sin4 x +C.
Пример 8. Вычислить несобственные интегралы или доказать их расходимость.
1) 
x 3 -x dx; 2) 
.
Решение.
Несобственный интеграл от функции f (x) в пределах от а до +¥ определяется равенством
Если этот предел существует и конечен, то несобственный интеграл называется сходящимся, если же предел не существует или равен бесконечности - расходящимся
|
|
|
1) 
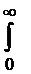x 
dx= 
Несобственный интеграл сходится
2) 
= 
= 
= 
=
= 
= 
= 
.
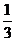
Следовательно, интеграл расходится.
Пример 9. Вычислить площадь фигуры, ограниченной линиями: y= 5 − x2; y=x+ 3.
Решение. Сделаем чертеж (рис.4). Найдем абсциссы точек пересечения линий: y= 5 −x2, y=x+ 3. Для этого приравняем правые части уравнений
5 −x2=x+ 3.
Решая полученное уравнение, найдем
x 1 =− 2, x 2 = 1.
Bоспользуемся формулой площади криволинейной трапеции, ограниченной линиями y=y(x), x=a, x=b, y= 0:
S= 
y(x)dx.
В нашем случае площадь фигуры можно получить как разность площадей S1 и S2 двух криволинейных трапеций, ограниченных линиями y= 5 −x2 и y=x+ 3, соответственно. В результате получим
S=S1−S2= 
(5 −x2) dx − 
(x+ 3) dx= 
(2 −x−x 2) dx =
= (2 x −x 2 / 2 − x3/ 3) 
= (2 − 1/2 − 1/3) − (− 4 − 1/2+8/3) = 4,5.
Пример 10. В ычислить площадь фигуры, ограниченной линией
=a sin6 
(a> 0).
Решение. Для построения графика линии, заданной в полярной системе координат (
, ) уравнением вида 
= 
(), необходимо вначале установить при каких значениях полярного угла 
выполняется неравенство ( ) 0, обусловленное тем, что полярный радиус 
, являясь расстоянием от начала координат, всегда неотрицателен. В нашем случае sin6 0, откуда
2 
n 
6 2 n+ или n/ 3 n/ 3+ / 6. Здесь достаточно ограничиться значениями n =0,1,2,3,4,5, т.к. при других значениях n с точностью до целого числа полных оборотов полярного луча для будет получаться то же самое. Задаваясь значениями i (i= 1,2...) и вычисляя соответствующие i= ( i)можно построить график линии (рис.5) Ограниченная этим графиком фигура называется шестилепестковой розой. Отметим, что линия = a sin k является графиком k -лепестковой розы, первый лепесток которой соответствует 
[0, /k ]. В случае =a cos k , т.е. =a sin k ( + / 2 k) мы имеем дело с той же k- лепестковой розой, только повернутой на угол / 2 k по часовой стрелке. Для нахождения площади фигуры, ограниченной линией = ()и двумя лучами = 
, = 
, (
< 
) используется формула
S= 
2( ) d
|
|
|
В нашем случае достаточно вычислить площадь одного лепестка (0 / 6) и ушестерить ее. Поэтому
S= 6 a 2sin26 d =
= 3 a2 
(1 − cos12 )/2 d = 3/2 a2 ( − sin12 /12) = a 2/4
Пример 11. Вычислить длину дуги кривой, заданной уравнением:
у= 
, 0 
3.
Решение.
Длина дуги кривой, заданной уравнением y= f(x) при а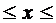 
в, вычисляется по формуле
L= 
В рассматриваемом случае 
L= 3 
= 3 arcsin (x /3) 
= 3 (arcsin 1 − arcsin 0) = 3 /4.
Пример 12. Вычислить длину дуги кривой, заданной параметрическими уравнениями: x= cos t+ ln tg (t/2); y= sin t, причем / 4< t< / 2.
Решение. Если линия задана параметрически, т.е. уравнениями вида x=x(t); y=y(t), то длина L этой линии, соответствующей t 
вычисляется с помощью формулы
L= 
В рассматриваемом случае
L= 
= ctg t dt= ln 
= ln(
)=ln 
.
Здесь учтено, что при / 4 t / 2, ctg t> 0, 
Пример 13. Вычислить объем тела. Которое получается при вращении вокруг оси ОX фигуры, ограниченной линиями:
у= 1+1/ х; х= 1; х= 3; у= 0.
Решение. Сделаем чертеж (рис.6). Воспользуемся формулой объема тела, полученного от вращения вокруг вокруг оси ОX криволинейной трапеции, ограниченной линиями у=у(х), х=а, х=в, у= 0:
V=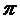 
y 2 (x)dx.
В нашей задаче объем тела равен
V= 
= 
= (x+ 2ln x− 1/ x) 
=
= (3+2ln3 − 1/3) − (1+2ln1 − 1) = 
(8+6 ln3) (куб.ед).
Приложение
Таблица интегралов
. 
.
. 
.
. 
.
. 
.
. 
.
.
