Пример 1. Определить на отрезке [ – 3; 3/2] наибольшее и наименьшее значения функции y = x 3 – 3 x+ 3.
Решение. Если искомое значение достигается внутри отрезка, то это значение будет одним из экстремумов. Но может случиться, что наибольшее и наименьшее значения достигаются на концах отрезка.
1) Находим максимумы и минимумы функции на отрезке [ – 3;3/2]. Из условия  = 0 находим критические точки.
= 0 находим критические точки.
 = 3 x2 – 3 =0; x1 = 1; x2 = – 1 .
= 3 x2 – 3 =0; x1 = 1; x2 = – 1 .
Проверяем достаточное условие  = 6 х, тогда
= 6 х, тогда  (1)=6 >0. Следовтельно, в точке х= 1 имеет место минимум: у (1) =1.
(1)=6 >0. Следовтельно, в точке х= 1 имеет место минимум: у (1) =1.
Далее,  (– 1)= – 6< 0. Следовательно, в точке х= – 1 имеет место максимум у (– 1) = 5.
(– 1)= – 6< 0. Следовательно, в точке х= – 1 имеет место максимум у (– 1) = 5.
2) Определяем значения функции на концах отрезка:
у (– 3)= – 15, у (3/2) = 15/8. Таким образом, наибольшее значение рассматриваемой функции на отрезке [ – 3;3/2] есть у (– 1) = 5, а наименьшее значение – у (– 3) = – 15.
Пример 2. Найти высоту прямого конуса с наименьшим объемом, описанного около шара данного радиуса R.
Решение. Найдем зависимость объема конуса от его высоты H. Проведем сечение плоскостью, проходящей через высоту конуса BК (Рис. 1).
V= 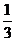
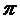 r 2 H.
r 2 H.
Здесь r = AК – радиус основания конуса. Пусть  ABК =
ABК =  . OC
. OC  AB как радиус, проведенный в точку касания.
AB как радиус, проведенный в точку касания.
Из  АВК r=H tg
АВК r=H tg  , V=
, V= 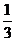
 H 3 tg2
H 3 tg2  . Найдем tg2
. Найдем tg2  .
.

 OBC: sin
OBC: sin  =
=  =
=  , cos2
, cos2  =1 –
=1 –  . tg2
. tg2  =
=  ,
,
V= 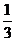

 .
.
Найдем область определения получнной функции. Так как из геометрического смысла V> 0, то Н >2 R, то есть функция опрелелена на интервале (2R;  ). Следовательно, функция
). Следовательно, функция  принимает наименьшее значение во внутренних точках минимума интервала.
принимает наименьшее значение во внутренних точках минимума интервала.
Найдем производную
 =
= 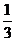
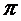
 .
.
 =0 при H= 0, H= 4 R. Следовательно, при этих значениях Н функция V может иметь экстремум. Найдем вторую производную
=0 при H= 0, H= 4 R. Следовательно, при этих значениях Н функция V может иметь экстремум. Найдем вторую производную
 =
= 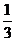
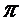
 .
.
T.к. H >2 R,  >0 и при H= 4 R
>0 и при H= 4 R  объем конуса будет наименьшим.
объем конуса будет наименьшим.
Пример 3.
Составить уравнения касательной и нормали к кривой в точке, соответствующей значению параметра 

Решение. Если кривая задана уравнением у = f (х), то
 где α – угол, образованный с положительным направлением оси ОX касательной к кривой в точке с абсциссой
где α – угол, образованный с положительным направлением оси ОX касательной к кривой в точке с абсциссой  .
.
Уравнение касательной к кривой у = f (х) в точке  имеет вид
имеет вид
 .
.
Нормалью к кривой называется прямая, перпендикулярная к касательной и проходящая через точку касания.
Уравнение нормали имеет вид
 .
.
Кривая в примере задана параметрически. Найдем ее производную  .
.

При  . Найдем значения
. Найдем значения  .,
.,  , соответствующие
, соответствующие  . Получим
. Получим  =0,
=0,  =0.
=0.
Уравнение касательной у=х, уравнение нормали у= −х.
Пример 4. Исследовать методами дифференциального исчисления функцию у = f (х) и, используя результаты исследования, построить ее график
y = x3 / 2 (x+ 1)2
Решение. Полное исследование функций будем проводить, придерживаясь плана:
1) найти область определения функции;
2) найти точки разрыва;
3) отметить простейшие свойства (четность, периодичность, пересечение с осями);
4) асимптоты (вертикальные, наклонные);
5) критические точки первого рода (из условия  (x)=0 или
(x)=0 или  (x)`- не существует);
(x)`- не существует);
6) критические точки второго рода (из условия  (x)=0 или
(x)=0 или  (x) не существует);
(x) не существует);
7) интервалы возрастания и убывания;
8) экстремумы;
9) интервалы выпуклости и вогнутости, точки перегиба.
На основании проведенного исследования строится график функции.
1. Найдем область определения функции.
Поскольку f(x) представляет собой дробь, знаменатель дроби должен быть отличен от нуля, х+ 1=0; х = − 1. Таким образом,
D (y) = (−  .
.
2. Определяем точки пересечения графика функции с координатными осями. Единственной такой точкой будет точка О (0,0).
3. Исследуем функцию на четность или нечетность

Очевидно, что у(−х) ¹ у (х) и у(−х) ¹ −у(х), поэтому функция не является ни четной, ни нечетной. Рассмотрим периодичность функции. Функция не является периодической.
4. Исследуем функцию на наличие у ее графика асимптот.
а) Вертикальные асимптоты.
Вертикальную асимптоту можно искать лишь в виде х = -1. Для доказательства, что эта вертикальная прямая будет асимптотой вычислим пределы справа и слева при  от функции f(x):
от функции f(x):

 = −
= −  ;
; 

 = −
= −  .
.
Поскольку среди найденных пределов получились бесконечности, то х= − 1 действительно будет вертикальной асимптотой.
б) Наклонные асимптоты.
Наклонные асимптоты будем искать в виде прямых линий с уравнениями у = kх+ в при  .
.
k =  1/2;
1/2;


Таким образом, прямая с уравнением у=х/2 − 1 является асимптотой при  . Те же самые значения пределов для k и b получим и при
. Те же самые значения пределов для k и b получим и при  , поэтому найденная прямая является асимптотой и при
, поэтому найденная прямая является асимптотой и при  .
.
5. Найдем интервалы возрастания, убывания функции, точки экстремума. Для этого найдем производную функции  .
.
 =
=  .
.
Стационарными точками являются х = 0, х = − 3, при которых  = 0. Других критических точек, отличных от стационарных, у функции нет. При
= 0. Других критических точек, отличных от стационарных, у функции нет. При  > 0 функция возрастает, при
> 0 функция возрастает, при  < 0 убывает.
< 0 убывает.
6. Найдем интервалы выпуклости и вогнутости, точки перегиба. Для этого найдем вторую производную

 .
.
Точкой, где  может менять знак, является точка х = 0, следовательно, х = 0 является точкой перегиба. Если
может менять знак, является точка х = 0, следовательно, х = 0 является точкой перегиба. Если  < 0, функция выпукла, при
< 0, функция выпукла, при  > 0 - вогнута.
> 0 - вогнута.
7. Результаты исследования знаков производных и соответствующего поведения функции на интервалах оформляем в виде таблицы.
| x | ( ) )
| − 3 | (−3,−1) | −1 | (−1,0) | 0 | (0,∞) |

| + | 0 | − | Не сущ. | + | 0 | + |

| − | − | Не сущ. | − | 0 | + | |
| у | Возр., вып. | Мах
у = 
| Убыв., вып. | Не сущ. | Возр., вып. | Точка перег. | Возр., вогн. |
8. Строим график функции, нанося предварительно асимптоты, точки пересечения графика с координатными осями, точки экстремума и перегиба графика и соединяя их плавной кривой (рис. 2).

Пример 5 Исследовать методами дифференциального исчисления функцию у = f (х) и, используя результаты исследования, построить ее график

1. Найдем область определения функции. Из областиопределения логарифма следует
 .
.
Таким образом, D (y) = (−  .
.
2. Определяем точки пересечения графика функции с координатными осями. Так как х = 0 не входит в обдасть определения функции, то точек пересечения с осью ОY нет. Найдем точку пересечения с осью ОX:

Таким образом ( ) – точка пересечения с осью ОX.
) – точка пересечения с осью ОX.
3. Исследуем функцию на четность или нечетность

Очевидно, что у (−х) ¹ у (х)и у (−х) ¹ −у (х), поэтому функция не является ни четной, ни нечетной. Рассмотрим периодичность функции. Функция не является периодической.
4. Исследуем функцию на наличие у ее графика асимптот.
а) Вертикальные асимптоты.
Вертикальные асимптоты можно искать лишь в виде х = -3 и х= 0. Для доказательства, что эти вертикальные прямые будут асимптотами вычислим односторонние пределы при  от функции f(x):
от функции f(x):


Поскольку среди найденных пределов получились бесконечности  действительно будут вертикальными асимптотами.
действительно будут вертикальными асимптотами.
б) Наклонные асимптоты.
Наклонные асимптоты будем искать в виде прямых линий с уравнениями у = kх+ в при  .
.
k = 

Так как k= 0, то наклонных асимптот нет, прямая у = −1 является горизонтальной асимптотой.
5. Найдем интервалы возрастания, убывания функции, точки экстремума. Для этого найдем производную функции  .
.
 =
= 

 0 при любом х из области определения функции;
0 при любом х из области определения функции;  не существует при х = -3 и х= 0. Эти точки не входят в область определения функции0. При
не существует при х = -3 и х= 0. Эти точки не входят в область определения функции0. При  > 0 функция возрастает, при
> 0 функция возрастает, при  < 0 убывает.
< 0 убывает.
6. Найдем интервалы выпуклости и вогнутости, точки перегиба. Для этого найдем вторую производную

 .
.
Точкой, где  может менять знак, является точка х =−3/2, которая не входит в область определения функции, следовательно, точек перегиба нет. Если
может менять знак, является точка х =−3/2, которая не входит в область определения функции, следовательно, точек перегиба нет. Если  < 0, функция выпукла, при
< 0, функция выпукла, при  > 0 - вогнута.
> 0 - вогнута.
7. Результаты исследования знаков производных и соответствующего поведения функции на интервалах оформляем в виде таблицы.
| x | ( ) )
| (0,∞) |

| − | − |

| − | + |
| у | Убывает, выпуклая. | Убывает, вогнутая. |
8. Строим график функции, нанося предварительно асимптоты, точки пересечения графика с координатными осями, точки экстремума и перегиба графика и соединяя их плавной кривой (рис. 3).
 |
 2018-02-12
2018-02-12 250
250








