Лекція № 5.
Тема 4. КІНЕМАТИКА СКЛАДНОГО РУХУ ТОЧКИ
Основні поняття
 Рух точки
Рух точки  називається складним, якщо вона одночасно бере участь у декількох рухах. Нехай тіло
називається складним, якщо вона одночасно бере участь у декількох рухах. Нехай тіло  рухається відносно нерухомої системи координат
рухається відносно нерухомої системи координат  , а по тілу
, а по тілу  рухається точка
рухається точка  . Рух точки
. Рух точки  є складним.
є складним.
На тілі  виберемо систему координат
виберемо систему координат  , жорстко зв’язану з цим тілом. Система координат
, жорстко зв’язану з цим тілом. Система координат  – рухома (рис. 4.1).
– рухома (рис. 4.1).
Рух точки  відносно нерухомого тіла, на якому вибрана нерухома система координат
відносно нерухомого тіла, на якому вибрана нерухома система координат  , будемо називати абсолютним рухом. При цьому русі точка
, будемо називати абсолютним рухом. При цьому русі точка  має абсолютну швидкість
має абсолютну швидкість  і абсолютне прискорення
і абсолютне прискорення  .
.
Рух точки  відносно рухомої системи координат
відносно рухомої системи координат  (тобто відносно рухомого тіла
(тобто відносно рухомого тіла  ) будемо називати відносним рухом. При цьому русі точка
) будемо називати відносним рухом. При цьому русі точка  має відносну швидкість
має відносну швидкість 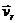 і відносне прискорення
і відносне прискорення  .
.
Рух тіла  разом з системою координат
разом з системою координат  відносно нерухомої системи координат
відносно нерухомої системи координат  є для точки
є для точки  переносним рухом, а швидкість і прискорення тієї точки тіла
переносним рухом, а швидкість і прискорення тієї точки тіла  , де в даний момент часу знаходиться точка
, де в даний момент часу знаходиться точка  , називається переносною швидкістю
, називається переносною швидкістю  і переносним прискоренням
і переносним прискоренням  .
.
Основною задачею кінематики складного руху точки є встановлення залежності між швидкостями і прискореннями в двох системах координат: нерухомій і рухомій.
Рівняння руху точки
Нехай точка  одночасно здійснює рух відносно нерухомої і рухомої системи координат. Як видно з рисунка 4.1, рівняння руху точки
одночасно здійснює рух відносно нерухомої і рухомої системи координат. Як видно з рисунка 4.1, рівняння руху точки  в векторній формі можна записати наступним чином:
в векторній формі можна записати наступним чином:
 . (4.1)
. (4.1)
Радіус-вектор  описує рух точки
описує рух точки  відносно нерухомої системи координат; радіус-вектор
відносно нерухомої системи координат; радіус-вектор  описує рух точки
описує рух точки  відносно рухомої системи координат; радіус-вектор
відносно рухомої системи координат; радіус-вектор  описує рух точки
описує рух точки  (початку рухомої системи координат) відносно нерухомої системи координат.
(початку рухомої системи координат) відносно нерухомої системи координат.
Радіус-вектор  точки
точки  можна представити в наступному вигляді:
можна представити в наступному вигляді:
 , (4.2)
, (4.2)
де 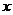 ,
, 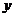 ,
, 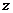 – координати точки
– координати точки  в рухомій системі координат
в рухомій системі координат  ;
;  ,
,  ,
,  – одиничні орти рухомої системи координат.
– одиничні орти рухомої системи координат.
При русі точки  її координати
її координати 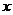 ,
, 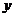 ,
, 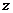 змінюються, тобто вони є функціями часу:
змінюються, тобто вони є функціями часу:
 ;
;  ;
; 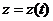 . (4.3)
. (4.3)
Рівняння (4.3) є рівняннями відносного руху точки  .
.
Початок  рухомої системи координат може переміщатися відносно нерухомої системи координат, тому
рухомої системи координат може переміщатися відносно нерухомої системи координат, тому
 . (4.4)
. (4.4)
Якщо тіло  здійснює обертальний рух навколо точки
здійснює обертальний рух навколо точки  , то рухома система координат також обертається і напрями одиничних ортів змінюються. Отже, у загальному випадку, одиничні орти є функціями часу:
, то рухома система координат також обертається і напрями одиничних ортів змінюються. Отже, у загальному випадку, одиничні орти є функціями часу:
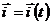 ,
,  ,
,  . (4.5)
. (4.5)
Рівняння (4.4) – (4.5) характеризують переносний рух рухомої системи координат.
З урахуванням (4.1) рівняння руху точки  можна записати у вигляді
можна записати у вигляді
 . (4.6)
. (4.6)
Теорема додавання швидкостей
Теорема. При складному русі точки її абсолютна швидкість  дорівнює геометричній сумі відносної
дорівнює геометричній сумі відносної 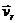 і переносної
і переносної  швидкостей
швидкостей
 . (4.7)
. (4.7)
Доведення. Нехай точка  здійснює складний рух. Візьмемо похідну по часу від виразу (4.6), врахувавши при цьому залежності (4.3), (4.4) і (4.5)
здійснює складний рух. Візьмемо похідну по часу від виразу (4.6), врахувавши при цьому залежності (4.3), (4.4) і (4.5)
 . (4.8)
. (4.8)
Так як  характеризує абсолютний рух точки
характеризує абсолютний рух точки  , то
, то  – абсолютна швидкість точки
– абсолютна швидкість точки  . Перший доданок, виділений дужками в правій частині, враховує рух рухомої системи координат відносно нерухомої, – переносна швидкість
. Перший доданок, виділений дужками в правій частині, враховує рух рухомої системи координат відносно нерухомої, – переносна швидкість  . Другий доданок, виділений дужками, враховує рух точки
. Другий доданок, виділений дужками, враховує рух точки  відносно рухомої системи координат, – відносна швидкість
відносно рухомої системи координат, – відносна швидкість 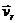 .
.
Теорема доведена.
 , (4.9)
, (4.9)
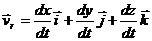 , (4.10)
, (4.10)
де  – швидкість точки
– швидкість точки  – початку рухомої системи координат відносно нерухомої.
– початку рухомої системи координат відносно нерухомої.
Розглянемо окремо вираз (4.9) для переносної швидкості  . У виразі (4.9) зустрічаються похідні по часу від одиничних ортів. Встановимо, чому дорівнюють похідні по часу від одиничних ортів. Ці похідні залежать від виду руху тіла
. У виразі (4.9) зустрічаються похідні по часу від одиничних ортів. Встановимо, чому дорівнюють похідні по часу від одиничних ортів. Ці похідні залежать від виду руху тіла  і пов’язаної з ним системи координат:
і пов’язаної з ним системи координат:
1. Нехай тіло  здійснює поступальний рух. Тоді одиничні орти
здійснює поступальний рух. Тоді одиничні орти  ,
,  ,
,  є постійними величинами, тому вираз (4.9) прийме вигляд
є постійними величинами, тому вираз (4.9) прийме вигляд  . Таким чином, при поступальному русі рухомої системи координат переносна швидкість точки
. Таким чином, при поступальному русі рухомої системи координат переносна швидкість точки  дорівнює швидкості точки
дорівнює швидкості точки  – початку рухомої системи координат.
– початку рухомої системи координат.
 2. Нехай відносно нерухомої точки
2. Нехай відносно нерухомої точки  система координат
система координат  здійснює обертальний рух (
здійснює обертальний рух ( ).Швидкість точки
).Швидкість точки  тіла, яке обертається відносно осі
тіла, яке обертається відносно осі  з кутовою швидкістю
з кутовою швидкістю  рівна
рівна  , де
, де 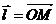 (рис. 4.2). Звідки маємо
(рис. 4.2). Звідки маємо

 . (4.11)
. (4.11)
Нехай рухома система координат  , закріплена тільки в одній точці
, закріплена тільки в одній точці  , обертається навколо осі
, обертається навколо осі  (миттєвої осі обертання) з кутовою швидкістю
(миттєвої осі обертання) з кутовою швидкістю  (рис. 4.3). Аналогічно виразу (4.11) маємо:
(рис. 4.3). Аналогічно виразу (4.11) маємо:
 ,
,  ,
,  , (4.12)
, (4.12)
де  – кутова швидкість переносного руху. Підставивши вираз (4.12) в (4.9), маємо:
– кутова швидкість переносного руху. Підставивши вираз (4.12) в (4.9), маємо: 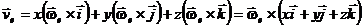 . Або
. Або
 . (4.13)
. (4.13)
Таким чином, якщо переносний рух є обертальним, то переносна швидкість точки  знаходиться за формулою Ейлера (4.13).
знаходиться за формулою Ейлера (4.13).
3. В загальному випадку, якщо точка  рухається зі швидкістю
рухається зі швидкістю  , а рухома система координат обертається навколо точки
, а рухома система координат обертається навколо точки  , то переносна швидкість точки
, то переносна швидкість точки  знаходиться з формули.
знаходиться з формули.
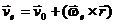 . (4.14)
. (4.14)
Формула (4.7) виражає правило паралелограма швидкостей. Відносна і переносна швидкості можуть бути напрямлені під різними кутами одна до одної. Модуль абсолютної швидкості точки  у загальному випадку визначається за формулою:
у загальному випадку визначається за формулою:
 . (4.15)
. (4.15)
1. Якщо  , то
, то
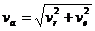 . (4.16)
. (4.16)
2. Нехай 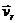 і
і  напрямлені в одну сторону. Тоді
напрямлені в одну сторону. Тоді
 . (4.17)
. (4.17)
3. Нехай 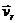 і
і  напрямлені протилежно. Тоді
напрямлені протилежно. Тоді
 . (4.18)
. (4.18)
Абсолютна швидкість  буде напрямлена в сторону більшої швидкості.
буде напрямлена в сторону більшої швидкості.
 2018-02-20
2018-02-20 1117
1117







