На границе раздела двух диэлектриков с разными диэлектрическими проницаемостями выполняются два следующих условия:
1) равны тангенциальные составляющие напряженности поля: 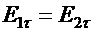 ;
;
2) равны нормальные составляющие вектора электрического смещения: 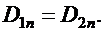
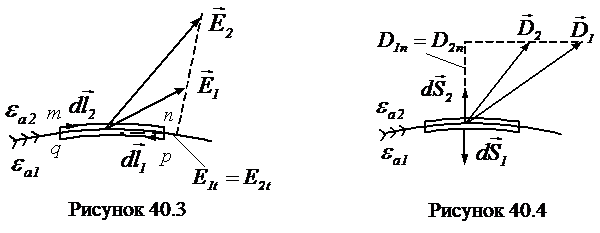
Докажем справедливость первого условия. Для этого выделим на границе раздела плоский замкнутый контур mnpqm (рис.40.3) и составим вдоль этого контура циркуляцию вектора напряженности электрического поля. Контур возьмем таким, чтобы стороны mq и np были бесконечно малы по сравнению с dl. Поэтому составляющими циркуляции вдоль этих сторон можно пренебречь. Составляющая 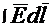 на пути mn равна
на пути mn равна 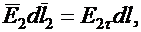 а по пути pq равна
а по пути pq равна 
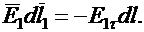 Знак минус появился потому, что элемент длины на пути pq и касательная составляющая вектора
Знак минус появился потому, что элемент длины на пути pq и касательная составляющая вектора 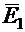 направлены в противоположные стороны. Таким образом,
направлены в противоположные стороны. Таким образом, 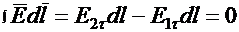 или
или 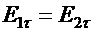 .
.
Для доказательства второго условия на границе раздела двух сред выделим параллелепипед очень малых размеров (рис.40.4).
Внутри выделенного объема есть связанные заряды и нет свободных, поэтому 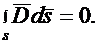
Поток вектора 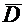 :
:
через верхнюю грань площадью ds: 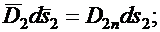 через нижнюю грань:
через нижнюю грань:
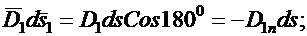
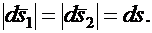 Следовательно,
Следовательно, 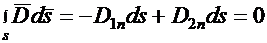 или
или 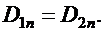
Теорема единственности решения
Электрическое поле описывается уравнениями Лапласа или Пуассона, которые являются дифференциальными уравнениями в частных производных и в отличие от обыкновенных дифференциальных уравнений имеют в общем случае множество линейно независимых друг от друга решений. В любой конкретной задаче должно быть единственное решение. Его можно найти, используя граничные условия.
Если есть некоторая функция, удовлетворяющая уравнению Лапласа – Пуассона граничным условиям в данном поле, то эта функция и представляет собой то единственное решение конкретной задачи, которое ищут.
Это положение называют теоремой единственности решения.
Поле заряженной оси

Под заряженной осью понимают тонкий бесконечно длинный металлический проводник. Заряд на единицу длинный проводника обозначим через τ. Диэлектрическая проницаемость среды, окружающей ось, равна 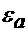 . Для нахождения напряженности поля в некоторой точке, удаленной на расстояние r от оси (рис.40.5), проведем через эту точку цилиндрическую поверхность так, что ось цилиндрической поверхности совпадает с заряженной осью.
. Для нахождения напряженности поля в некоторой точке, удаленной на расстояние r от оси (рис.40.5), проведем через эту точку цилиндрическую поверхность так, что ось цилиндрической поверхности совпадает с заряженной осью.
Применим теорему Гаусса. Поток вектора 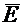 имеется только через боковую поверхность цилиндра. Через донышки поток отсутствует, так как элемент поверхности
имеется только через боковую поверхность цилиндра. Через донышки поток отсутствует, так как элемент поверхности 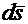 каждого донышка перпендикулярен
каждого донышка перпендикулярен 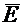 .
.
Элементы 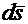 боковой поверхности и напряженность электрического поля
боковой поверхности и напряженность электрического поля 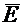 в любой точке цилиндрической поверхности по направлению совпадают, поэтому
в любой точке цилиндрической поверхности по направлению совпадают, поэтому
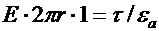 или или 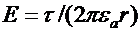 . .
| (40.3) |
Напряженность в поле заряженной оси изменяется обратно пропорционально расстоянию r точки от оси. Потенциал
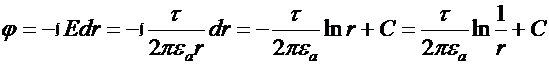
| (40.4) |
изменяется по логарифмическому закону.
 2018-02-13
2018-02-13 360
360








