Уравнение прямой в декартовых координатах

УДК 514.12(075.8)

ББК В151.54я73

ВВЕДЕНИЕ

В методической разработке рассмотрены уравнения прямой на плоскости в декартовой прямоугольной системе координат. Приведены задачи с подробным решением и задания для самостоятельной работы.

Пособие может быть использовано как на практических занятиях по математике и аналитической геометрии, так и в самостоятельной работе студентов при подготовке к экзамену.

1. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ
НА ПЛОСКОСТИ

Возьмем на плоскости произвольную прямую и отметим на этой прямой некоторую точку О, называемую началом отсчета. Теперь будем двигаться по прямой в одном из направлений от точки отсчета, считая это направление положительным (это положительное направление отмечают стрелкой). Тогда движение в противоположном направлении от точки О будет называться отрицательным. Прямая, на которой указано положительное направление, называется осью. Если теперь на оси выбрать единицу измерения, то мы получим числовую ось (каждому действительному числу будет соответствовать единственная точка числовой оси). Если числовая ось изображена горизонтальной линией, то положительным направлением обычно считают движение слева направо (рис. 1).

Теперь каждая точка на оси определяется числом, называемым координатой этой точки. На рис. 1 точка М имеет координату 3 (запись М(3)).

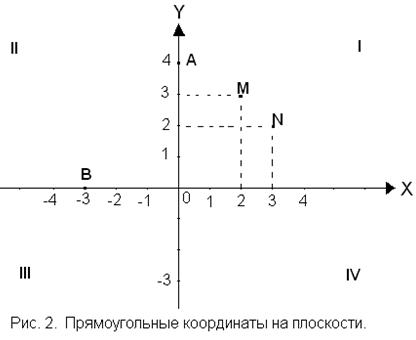
Для определения положения точки на плоскости одной оси недостаточно. Требуются две пересекающиеся оси с общим началом отсчета и одинаковой единицей измерения. Удобнее всего положение точки определять относительно двух взаимно перпендикулярных осей, называемых координатными осями. Одна из осей называется осьюабсцисс и обозначается ОХ, а другая – осью ординат и обозначается ОУ. Такая система координат ХОУ называется декартовыми прямоугольными координатами на плоскости. Обычно ось ОХ изображают горизонтально, а ось ОУ – вертикально (рис. 2).

Точка О называется началом координат. Координатные оси делят всю плоскость на четыре угла, которые называются либо координатными углами, либо квадрантами, либо четвертями. Квадранты нумеруются в направлении против часовой стрелки, как указано на рис. 2.

Первому квадранту соответствуют значения ;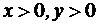

второму квадранту – значения ;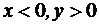

третьему квадранту – значения ;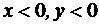

четвертому квадранту – значения .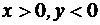

Положение произвольной точки М на плоскости в декартовой прямоугольной системе координат определяют следующим образом. Из точки М опускают перпендикуляр на ось ОХ и фиксируют точку на оси, соответствующую основанию перпендикуляра – это координата 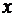. Теперь опустим перпендикуляр на ось ОУ и получим координату 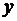. Эти два значения 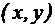полностью определяют положение точки М на плоскости. Таким образом, точка М определена своими проекциями на координатныеоси. Указывая координаты точки, принято первой указывать координату 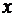, а второй – координату 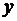: 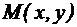. Пара, в которой определен порядок, называется упорядоченной. Пары (2–3) и (3–2) определяют разные точки плоскости. На рис. 2 это точки М и N соответственно. Если точка лежит на оси абсцисс ОХ, то ее координата 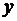(ордината) равна нулю. Если же точка лежит на оси ординат ОУ, то ее координата 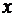(абсцисса) равна нулю. На рис. 2 точки А и В имеют координаты А(0;4), В(-3;0). Начало координат точка О имеет нулевые координаты: О(0;0).

Таким образом, каждой точке плоскости соответствует пара чисел – ее координаты. А каждой паре чисел соответствует единственная точка плоскости.

Метод координат позволяет решать геометрические задачи алгебраическими методами. Геометрия, использующая при решении задач такие методы, называется аналитической.

2. ОТРЕЗОК. ДЛИНА ОТРЕЗКА.
ДЕЛЕНИЕ ОТРЕЗКА В ДАННОМ ОТНОШЕНИИ

Отрезок прямой определяется двумя точками – его концами А и В, и обозначается [АВ] или [ВА], или АВ. Если А и В – различные точки, то отрезок [AB] единственным образом определяет прямую (АВ). В этом случае, говоря об отрезке, как о множестве точек, считают, что это множество состоит из точек А и В, а также точек, которые лежат на прямой (АВ) между точками А и В. Если выбрана единица измерения, то каждому отрезку [AB] можно сопоставить неотрицательное число 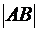, которое называется его длиной или расстоянием между точками А и В. Длину отрезка 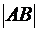также обозначают буквам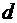и или 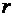. Если точки А и В заданы своими координатами, то длину отрезка можно вычислить по теореме Пифагора.

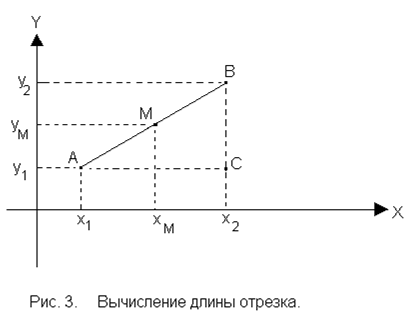
Пусть даны точк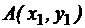и и 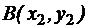(рис. 3). Длина проекции отрезка [AB] на ось ОХ составляет 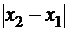, а длина проекции на ось ОУ составляет 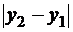. Таким образом, в прямоугольном треугольнике АВС известны длины двух катетов: 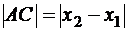, 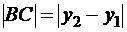. Тогда длина гипотенузы определяется формуло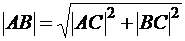й или

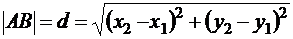. (2.1)

Если точка А совпадает с началом координат О, то длина отрезка [OB]

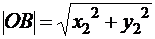. (2.2)

Пример 1. Даны точки А(2;6) и В(-1;2). Найти расстояние между ними.

Решение. По условию 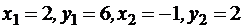, поэтому согласно формуле (2.1) .

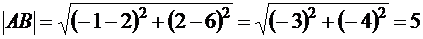Пусть теперь на отрезке [AB] зафиксирована точка М (рис.3) таким образом, что 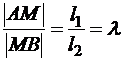. Попробуем найти координаты этой точки 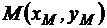. Поскольку проекции отрезка делятся точкам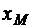и и 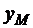в том же отношении, в котором точка М делит отрезок [AB], то можно записать , .

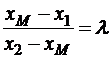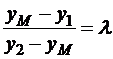Из полученных соотношений найдем 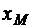и :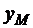

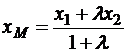, (2.3)

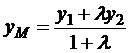. (2.4)

В частности, если точка М ─ середина отрезка, то 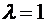, и

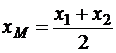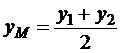, . (2.5)

Пример 2. Даны вершины треугольника А(-22;12), В(34;45), С(-2;-3). Вычислить периметр треугольника АВС. Найти координаты точки пресечения медиан треугольника.

Решение. Периметром Р называется сумма длин всех сторон многоугольника, поэтому 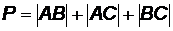. Проведем нужные вычисления:

;

; .

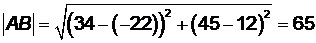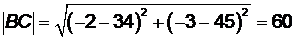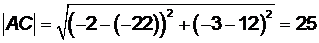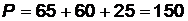Пусть 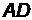− медиана треугольника АВС. Следовательно, точка 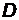− середина отрезка [BC] и ее координаты могут быть найдены по формулам (2.5): 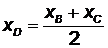, 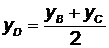. Подставим численные значения 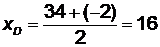. 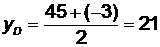; координаты точки .

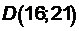Известно, что все три медианы треугольника пересекаются в одной точке М, которая делит каждую медиану в отношении 2:1, считая от вершины. Поэтому для медианы 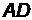можно записать соотношение: 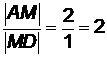. Теперь, используя формулы (2.3) и (2.4) деления отрезка в данном отношении при 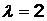, можно записать 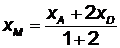, 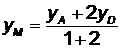. Подставив числовые значения, получим 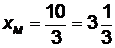, 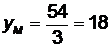. Координаты точки пересечения медиан .

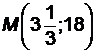Ответ: , .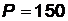

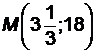Пример 3. Найти две точки А и В, если известно, что точка С(-5;4) делит отрезок [AB] в отношении 3:4, а точка D(6;-5) − в отношении 2:3.

Решение. Пусть точки А и В имеют координаты 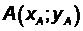и 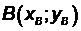. Тогда, согласно формулам (2.3) и (2.4), ; .

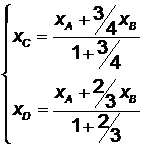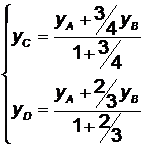Подставим числовые значения и получим две линейные системы с двумя неизвестными

, .

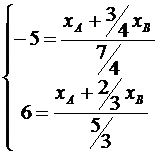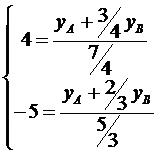Решая данные системы, получим , , , .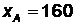

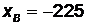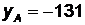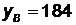Ответ: А(160;-131), В(-225;184).

Замечание. Рассматривать задачу деления отрезка в данном отношении можно и в том случае, когда точка М располагается не между точками А и В, а лежит на прямой (АВ) вне отрезка [AB]. В этом случае число 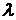отрицательное.

УРАВНЕНИЕ ПРЯМОЙ В ДЕКАРТОВЫХ КООРДИНАТАХ

Положение прямой вполне определено, если заданы какие-либо две ее точки или дана одна точка и указано направление прямой.

Пусть на прямой АВ зафиксированы две точк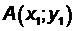и и .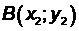

Выбранная на этой же прямой произвольная точка 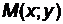делит отрезок [AB] в некотором отношении. Тогда справедливо равенство

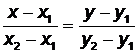, (3.1)

которое называется уравнением прямой, проходящей через две данныеточки плоскости. Если обозначить 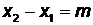, , 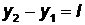то получим

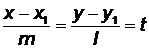или 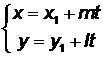− (3.2)

параметрическое уравнение прямой на плоскости.

Замечание. Формулы (3.1) и (3.2) следует понимать как пропорции, в которых значения 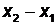и 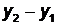могут быть равны нулю.

Пример 1. Даны вершины треугольника АВС: А(1;3). В(4;0), С(-4;3). Записать уравнения его сторон.

Решение. Используем формулу (3.1) и запишем:

(АВ): , , , .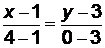

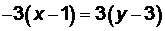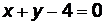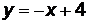(АС): , , , .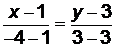

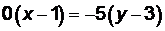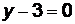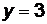(ВС): , , , .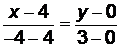

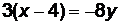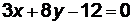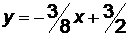Ответ. (АВ): 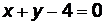; (АС): 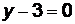; (ВС): .

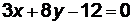Как видно из предыдущего примера, преобразование выражения (3.1) приводит к уравнению

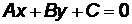, (3.3)

которое называется общим уравнением прямой. Это алгебраическое уравнение первой степени относительно двух переменных, называемое также линейным уравнением.

Таким образом, уравнение всякой прямой можно записать в виде (3.3), где А и В одновременно не равны нулю. Верно и обратное, т.е. уравнение (3.3) всегда определяет прямую.

Зная уравнение прямой, можно её построить, произвольно задавая две какие-либо её точки.

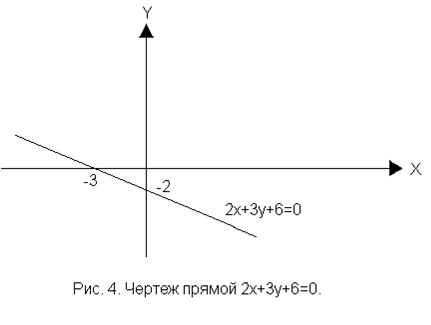
Пример 2. Дано общее уравнение прямой 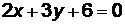. Построить эту прямую.

Решение. Возьмем два произвольных значения 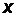и вычислим соответствующие значения 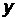. Пусть 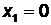, тогда 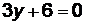, 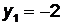. Пусть 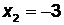, тогда 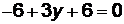, 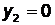. Таким образом, прямая проходит через точки (0;-2) и (-3;0) (рис. 4).

Рассмотрим частные случаи уравнения (3.3), в которых какие-либо из коэффициентов А, В, С равны нулю:

1) если прямая проходит через начало координат, то в уравнении (3.3) : ;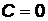

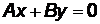2) если прямая параллельна оси абсцисс ОХ, то 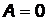: 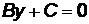или ;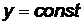

3) если прямая параллельна оси ординат ОУ, то 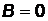: 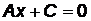или ;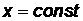

4) уравнение 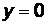определяет ось ОХ (одновременно выполняются условия 1) и 2)). Уравнение 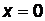определяет ось ОУ.

Пример 3. Уравнение 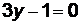определяет прямую, проходящую через точку 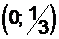параллельно оси абсцисс. Уравнение 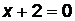определяет прямую, проходящую через точку (-2;0), параллельно оси ординат. Прямая 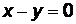проходит через начало координат и представляет собой биссектрису первого и третьего координатных углов.

Если в общем уравнении прямой (3.3) коэффициент В не равен нулю, то уравнение (3.3) можно привести к виду

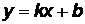, (3.4)

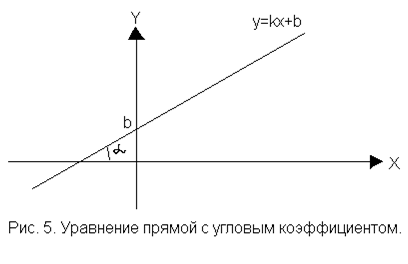
которое называется уравнением прямой с угловым коэффициентом.

Действительно, решая относительно 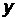уравнение (3.3), получим 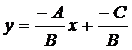. Обозначая 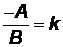, , 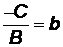приходим к уравнению (3.4).

Пример 4. Дано общее уравнение прямой 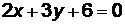. Записать его как уравнение с угловым коэффициентом.

Решение. Запишем уравнение в виде 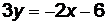, откуда , , .

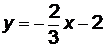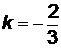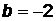Числа 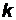и 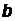в уравнении (3.4) имеют вполне определенный геометрический смысл. Угловой коэффициент 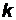− это тангенс угла, образованного прямой с положительным направлением оси ОХ (отсчет ведется от оси абсцисс в направлении против часовой стрелки): 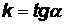. Число 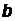показывает ординату пересечения прямой с осью ОУ (рис. 5).

Таким образом, два параметра 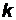и 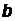полностью определяют положение прямой. Случай 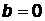соответствует прямой 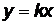, проходящей через начало координат. Случай 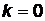определяет прямую 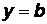, параллельную оси ОХ и проходящую через точку .

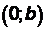Если теперь мы вернемся к уравнению прямой, проходящей через две заданные точки (3.1), то, записав его в виде 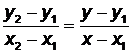, заметим, что отношение 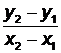есть не что иное, как тангенс угла наклона прямой к оси абсцисс, т.е. 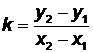. Теперь уравнение (3.1) можно переписать в виде

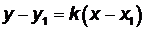. (3.5)

которое является уравнением прямой, проходящей через заданную точку 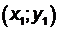. Задавая различные значения 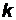, мы получим все прямые, проходящие через точку 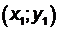. Поэтому уравнение (3.5) еще называют уравнением пучка прямых с центром в точке .

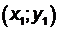Пример 5. Уравнение 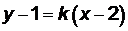определяет любую прямую, проходящую через точку (2;1). Выбирая различные значения 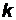, получим частные случаи прямых, проходящих через данную точку. Так, если 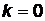, то уравнение 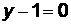определяет прямую, параллельную оси абсцисс. Если 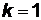, получим 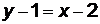или 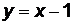, и т.д.

Если в общем уравнении прямой (3.3) все коэффициенты А, В, С отличны от нуля, то удобно преобразовать уравнение 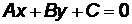к виду

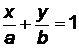, (3.6)

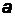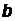которое называется уравнением прямой в отрезках. Числа и представляют собой координаты пересечения прямой с осями ОХ и ОУ соответственно. Переход от уравнения (3.3) к уравнению (3.6) выполняется так. Записав уравнение 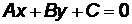в виде 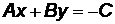, делим обе части полученного уравнения на 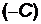: 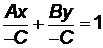или 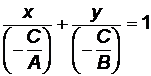. Обозначив, 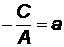, , 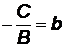получим (3.6).

Пример 6. Привести уравнение прямой 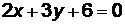к уравнению в отрезках.

Решение. Записав 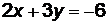, делим обе части равенства на (-6), получаем 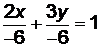или 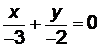. Прямая пересекает ось ОХ в точке
(-3;0), а ось ОУ − в точке (0;-2) (см. рис. 4).