Этапы решения задач с помощью симплекс-метода с естественным базисом

 

1. Привести задачу к канонической форме (знаки «=» в функциональных ограничениях и х_i ≥ 0).

2. Записать матрицу функциональных ограничений так, чтобы в её составе была единичная матрица. При этом получаем допустимое решение.

3. Проверить допустимое решение на оптимальность с помощью симплекс-разности: Δ_j = Σ c_ia_ij - с_j.

Если для всех векторов Δ_j ≥ 0, то решение оптимально.

4. Если решение неоптимальное, то в него вводим вектор (А_к), дающий минимальную величину симплекс-разности Δ_к (к - номер разрешающего столбца).

Если все компоненты вводимого в базис вектора ≤ 0, то задача решений не имеет.

5. Определить вектор (А_r), который должен быть выведен из базиса, для этого вычислить отношение Q = min  = , где  ≥ 0, (r – номер разрешающей строки).

Элемент а_rk – разрешающий элемент.

6. Пересчитать элементы матрицы функциональных ограничений по формулам:

 →                                   →

                                          

→                      →

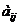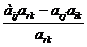
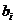(Проиллюстрировать правило прямоугольника.)

 

Примечание. Для использования приведенной процедуры к минимизации линейной функции f (x₁,x₂,…, x_n) следует искать максимум     «-f(x₁,x₂,…, x_n)», затем полученный максимум взять с противоположным знаком. Оптимальное решение то же.

 

Пример. Получить решение по модели: 

 

 

1 этап. Эта задача (модель) линейного программирования, приведем ее к каноническому виду путем введения дополнительных переменных x ₃ и x₄:

               

2 этап.

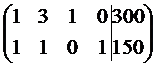Запишем матрицу коэффициентов функциональных ограничений.

 

 

КЗЛП имеет необходимое число единичных столбцов, т.е. обладает очевидным начальным опорным планом (0,0,300,150).

3 этап. Проверяется оптимальность полученного плана.

Расчеты  оформляются в симплекс-таблицах:

№	Базис	сi Сj	В план	2	3	0	0	Q
				А1	А2	А3	А4
	А3	0	300	1	3	1	0
0	А4	0	150	1	1	0	1
	Δ		0	-2	-3	0	0

 

Т.к. среди симплекс-разностей есть отрицательные, то полученный план не оптимален.

4 этап. Т.к. минимальная величина симплекс-разности соответствует вектору А₂, то он войдет в базис.

Второй столбец – разрешающий.

Этап.

Считаем величину Q.         Q = min  = , где  ≥ 0,

№	Базис	сi Сj	В план	2	3	0	0	Q
				А1	А2	А3	А4
	←А3	0	300	1	3	1	0	100
0	А4	0	150	1	1	0	1	150
	Δ		0	-2	-3	0	0

 

Т.к. минимальная величина Q соответствует вектору А₃, то выйдет из базиса вектор А₃. Первая строка - разрешающая. Элемент а₁₂ – разрешающий элемент.

 6 этап. Пересчитываем  элементы матрицы функциональных ограничений по формулам:

            

    

 

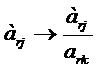
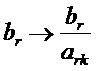
№	Базис	сi Сj	В план	2	3	0	0	Q
				А1	А2	А3	А4
	←А3	0	300	1	3	1	0	100
0	А4	0	150	1	1	0	1	150
	Δ		0	-2	-3	0	0
	А2	3	100	1/3	1	1/3	0	300
I	←А4	0	50	2/3	0	-1/3	1	75
	Δ		300	-1	0	1	0

Далее повторяем этапы 2-6 до получения оптимального решения.

 

№	Базис	сi  Сj	В план	2	3	0	0	Q
				А1	А2	А3	А4
	←А3	0	300	1	3	1	0	100
0	А4	0	150	1	1	0	1	150
	Δ		0	-2	-3	0	0
	А2	3	100	1/3	1	1/3	0	300
I	←А4	0	50	2/3	0	-1/3	1	75
	Δ		300	-1	0	1	0
	А2	3	75	0	1	1/2	-1/2
II	А1	2	75	1	0	-1/2	3/2
	Δ		375	0	0	1/2	3/2

 

В симплекс-таблице II получен оптимальный опорный план, поскольку все симплекс-разности неотрицательны.

 Оптимальные значения переменных равны: x1*=75, x2* =75 (основные переменные), x3*= 0, x4*= 0 (дополнительные переменные). Максимальное значение целевой функции равно 375.

 

Симплекс-метод с искусственным базисом (М-метод) применяется в тех случаях, когда затруднительно найти первоначальный опорный план канонической формы задачи ЛП.

 Этот метод заключается в применении правил симплекс-метода к так называемой М-задаче.

Она получается из исходной:

1. добавлением к матрице коэффициентов функциональных ограничений таких искусственных единичных векторов с соответствующими неотрицательными искусственными переменными, чтобы вновь полученная матрица содержала систему единичных, линейно-независимых векторов.  

2. в  линейную форму исходной задачи добавляется в случае ее максимизации слагаемое, представляющее собой произведение числа (-М) на сумму искусственных переменных, где М- достаточно большое число.

 

В полученной задаче первоначальный опорный план очевиден.

Как решать М-задачу: обычным симплекс-методом, но

1. В процессе решения М-задачи следует вычеркивать в симплекс-таблице искусственные векторы по мере их выхода из базиса. Если все искусственные векторы вышли из базиса, то получаем исходную задачу.

2.  Если в оптимальном решении М-задачи хотя бы одна из искусственных переменных отлична от нуля, то система ограничений исходной задачи несовместна (задача неразрешима). В случае неразрешимости М-задачи будет неразрешима и исходная задача (либо максимум бесконечен, либо условия задачи противоречивы).

Пример.

Решить ЗЛП по модели:

min f(х) = 10х₁ – 5х₂

2х₁ – х₂ ≥ 3

х₁ + х₂ ≥ 2

х₁ + 2х₂ ≥ -1

х_1,2  ≥ 0.

 1 этап. Эту ЗЛП приведем к каноническому виду и одновременно перейдем к задаче «на максимум».

max (- 10х₁ + 5х₂)

2х₁ – х₂ –х₃ = 3

х₁ + х₂  - х₄  = 2

-х₁ - 2х₂  + х₅  = 1

х_1,2,3,4,5  ≥ 0.

 

2 этап.

Запишем матрицу коэффициентов функциональных ограничений.

А₁  А₂ А₃   А₄ А₅

Если умножить на «-1» 1 и 2 строки, то станут отрицательными правые части (а это недопустимо)

Для нахождения опорного плана переходим к М - задаче: вводим искусственные единичные вектора в матрицу

А₁  А₂ А₃   А₄ А₅ Р₁   Р₂

Изменяем целевую функцию.

max (- 10х₁ + 5х₂ – Му₁ - Му₂)

Дальнейшее решение проводим в симплекс-таблицах:

 

 

Номер симплекс-таблицы	Базис	Сj   Сi	В	-10	5	0	0	0	-М	-М	Q
				А1	А2	А3	А4	А5	Р1	Р2
0	←Р1 Р2 А5	-М -М 0	3 2 1	2 1 -1	-1 1 -2	-1 0 0	0 -1 0	0 0 1	1 0 0	0 1 0	3/2 2 -
-	∆	-	-	-3М+10	-5	М	М	0	0	0	-
I	А1 ←Р2 А5	-10 -М 0	3/2 1/2 5/2	1 0 0	-1/2 3/2 -5/2	-1/2 1/2 -1/2	0 -1 0	0 0 1		0 1 0	- 1/3 -
-	∆	-		0	-3М/2	-М/2+5	М	0		0	-
II	А1 А2 А5	-10 5 0	5/3 1/3 10/3	1 0 0	0 1 0	-1/3 1/3 0	-1/3 -2/3 -5/3	0 0 1
-	∆	-	-	0	0	5	0	0			-

Полученный оптимальный план не единственный, т.к. нулевая оценка симплекс-разности соответствует вектору А₄, не входящему в базис.