Если вектор представлен через проекции на базисные векторы, то говорят о разложении вектора 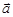 по ортогональному базису. Из рисунка видно, что в этом случае вектор
по ортогональному базису. Из рисунка видно, что в этом случае вектор 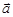 является главной диагональю прямоугольного параллелепипеда, ребра которого параллельны осям координат и равны длинам проекций вектора
является главной диагональю прямоугольного параллелепипеда, ребра которого параллельны осям координат и равны длинам проекций вектора 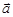 на эти оси. Из этого же рисунка следует, что модуль вектора
на эти оси. Из этого же рисунка следует, что модуль вектора 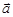 численно будет равен
численно будет равен
 .
.
Из определения скалярного произведения следует, что любой вектор, независимо от типа, можно представить в виде:
 ,
,
где  ,
,  и
и  есть скалярное произведение вектора
есть скалярное произведение вектора 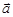 с ортами осей координат. Тогда из последнего равенства имеем
с ортами осей координат. Тогда из последнего равенства имеем

где a, b и g - углы, которые составляет вектор 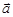 соответственно с осями 0х, 0у и 0z.
соответственно с осями 0х, 0у и 0z.
СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ.
Если скалярное произведение двух векторов равно нулю, то эти векторы ортогональны. Действительно, если ни один из векторов не нулевой, то, по определению скалярного произведения, последнее может быть равно нулю только тогда, когда 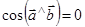 , т.е.
, т.е. 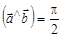 .
.
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ В КООРДИНАТНОЙ ФОРМЕ
Скалярное произведение векторов в координатной форме

 .
.
ТЕМА 3. Векторное произведение векторов. Смешанное произведение трех
Векторов.
ПРАВАЯ И ЛЕВАЯ ТРОЙКИ ВЕКТОРОВ
Линейно независимые векторы 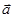 ,
, 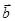 и
и 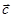 образуют правую тройку векторов, если они имеют такую же ориентацию, как соответственно большой, указательный и средний палец правой руки, в противном случае говорят о левой тройке векторов
образуют правую тройку векторов, если они имеют такую же ориентацию, как соответственно большой, указательный и средний палец правой руки, в противном случае говорят о левой тройке векторов
Три единичных вектора i, j, k, попарно ортогональные друг другу и образующие правую тройку векторов, называют прямоугольной декартовой системой координат.
Углом между векторами 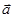 и
и 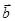 называют такой угол a, не превосходящий p, на который нужно повернуть вектор
называют такой угол a, не превосходящий p, на который нужно повернуть вектор 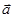 , чтобы совместить его с направлением вектора
, чтобы совместить его с направлением вектора 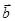 , начало которого должно совпадать с началом
, начало которого должно совпадать с началом 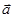 .Угол между векторами обозначается (
.Угол между векторами обозначается (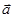 ,
, 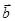 ) или (
) или (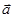 Ù
Ù 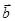 ).
).

 2020-01-14
2020-01-14 194
194








