Рассмотрим игру с платежной матрицей
A= 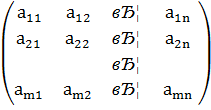 .
.
Если 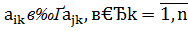 ,то говорят, что j -ая строка доминируется i -ой строкой, при этом i -ая строка называется доминирующей для первого игрока P 1; j -ая строка – доминируемой строкой для P 1.
,то говорят, что j -ая строка доминируется i -ой строкой, при этом i -ая строка называется доминирующей для первого игрока P 1; j -ая строка – доминируемой строкой для P 1.
Если 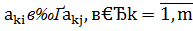 , то говорят, что i -ый столбец доминируется j -ым столбцом, при этом j -ый столбец называется доминирующим для второго игрока P 2; i -ый столбец – доминируемый для P 2. Доминируемую для игрока P 1 строку и доминируемый для P 2 столбец можно вычеркнуть (удалить).
, то говорят, что i -ый столбец доминируется j -ым столбцом, при этом j -ый столбец называется доминирующим для второго игрока P 2; i -ый столбец – доминируемый для P 2. Доминируемую для игрока P 1 строку и доминируемый для P 2 столбец можно вычеркнуть (удалить).
Пример. Упростить платежную матрицу A= 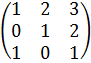 , используя принцип доминирования.
, используя принцип доминирования.
Решение.
1 способ: 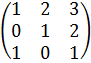 , т.к.
, т.к. 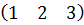 - доминирующая строка,
- доминирующая строка, 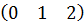 -
-
доминируемая строка 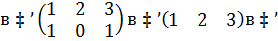 (1)
(1)
2 способ:, 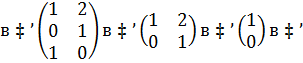 (1)
(1)
5.Решение матричной игры 2×2 в смешанных стратегиях
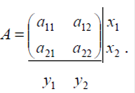
Решить игру с платежной матрицей
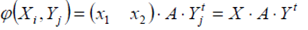
Платежная функция
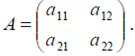
Решить игру с платежной матрицей
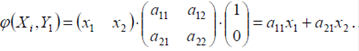
Положим 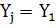 . Тогда
. Тогда
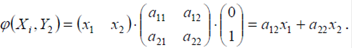
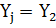 . Тогда
. Тогда
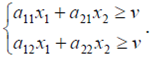 Если
Если 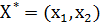 - оптимальная стратегия первого игрока, то по определению
- оптимальная стратегия первого игрока, то по определению
решения матричной игры
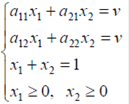 Если игра с нулевой суммой, то (
Если игра с нулевой суммой, то (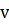 -цена игры).
-цена игры).
Решая систему, получим 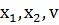 .
.
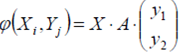
Аналогично для второго игрока:
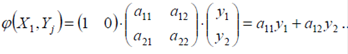
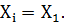 Тогда
Тогда
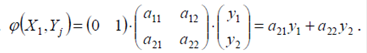
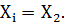 Тогда
Тогда
Если 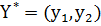 - оптимальная стратегия второго игрока.
- оптимальная стратегия второго игрока.
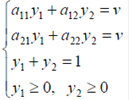 Если игра с нулевой суммой, то (
Если игра с нулевой суммой, то (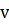 -цена игры).
-цена игры).
Решая систему, получим 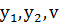 .
.
Пример. Найти решение игры заданной платежной матрицей A= 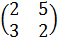 .
.
Решение:
Решим игру. Пусть 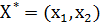 - оптимальная стратегия первого игрока,
- оптимальная стратегия первого игрока, 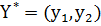 - оптимальная стратегия второго игрока,
- оптимальная стратегия второго игрока, 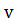 -цена игры. Тогда оптимальные стратегии игроков и цену игры можно найти, решив системы:
-цена игры. Тогда оптимальные стратегии игроков и цену игры можно найти, решив системы:
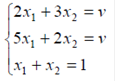
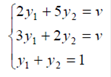
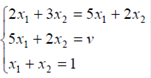
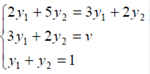
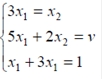
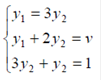
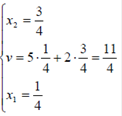
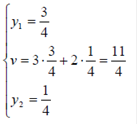
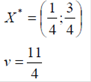
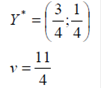
Ответ: оптимальные стратегии игроков 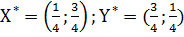 , цена игры
, цена игры 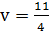 .
.
 2020-01-15
2020-01-15 506
506








