Знакозмінні та знакопостійні ряди.
План.
1. Означення закономірного ряду.
2. Теорема Коші.
3. Абсолютна та умовна збіжність.
Л-ра: Методичні вказівки до вивчення теми “Ряди”. Укладачі: В.О.Борисенко, В.В.Левчук, В.С.Мартиненко, В.Д.Подільчук. КДТЕУ. К, 1992 р. ст. 16-19.
Теорема. Якщо в ряді з додатними членами загальний член, починаючи з певного значення п, задовольняє нерівність 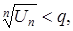 де q – стале число, менше за одиницю, то ряд збігається.
де q – стале число, менше за одиницю, то ряд збігається.
Коли ж навпаки, починаючи з певного значення п, маємо 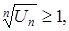 то ряд розбігається.
то ряд розбігається.
Доведення. У першому випадку маємо, починаючи з певного значення п, 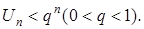
Отже, збіжність ряду й тут безпосередньо встановлюється порівнянням із спадною геометричною прогресією, знаменник якої q. Варто зауважити, що нерівність
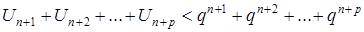
характеризує при цьому “швидкість” збіжностей даного ряду порівняно з геометричною прогресією.
В другому випадку матимемо з певного моменту 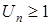 , отже, ряд напевне, розбігається, бо навіть основна необхідна умова збіжності не виконується.
, отже, ряд напевне, розбігається, бо навіть основна необхідна умова збіжності не виконується.
Наслідок. Якщо існує 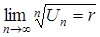 , то при r < 1 ряд напевне збігається. Випадок r = 1 і тут взагалі є сумнівний.
, то при r < 1 ряд напевне збігається. Випадок r = 1 і тут взагалі є сумнівний.
Доведення.
Взявши u тут якесь число q, проміжне між r та 1 (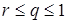 ), ми з певного моменту матимемо – в першому випадку:
), ми з певного моменту матимемо – в першому випадку:
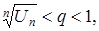
Отже, ряж збігається; а в другому: 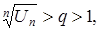 отже, ряд розбігається.
отже, ряд розбігається.
Часто питання про збіжність ряду, що має члени як додатні, так і від’ємні, можна звести до питання про збіжність знакододатного ряду. Розглянемо таку теорему.
Теорема. Ряди 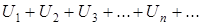 напевне збігається, якщо збігається ряд
напевне збігається, якщо збігається ряд 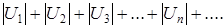
Доведення. Для кожного 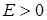 можна знайти таке
можна знайти таке 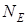 , при якому для
, при якому для 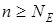 і при
і при 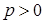 буде:
буде:
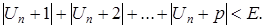
Але тоді й поготів
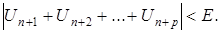
Але це й доводить теорему.
Означення. Збіжний ряд 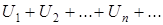 називається абсолютно збіжним. Якщо збігається також і ряд
називається абсолютно збіжним. Якщо збігається також і ряд 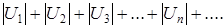
Розглянемо, наприклад, ряд
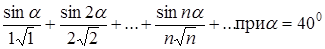 (1)
(1)
Він ні знакододатний, ні знакозмінний. Ряд
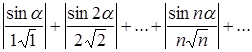 (2)
(2)
є знакододатний. Порівнюючи його з рядом
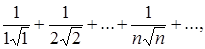 (3)
(3)
маємо
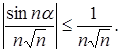
Ряд (3) збіжний, як ряд Діріхле-Рімана при 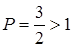 , отже, збіжним є ряд (2). Тоді за доведеною теоремою і за означенням ряд (1) є абсолютно збіжним.
, отже, збіжним є ряд (2). Тоді за доведеною теоремою і за означенням ряд (1) є абсолютно збіжним.
Оскільки ряд, члени якого – абсолютні значення членів будь-якого ряду є знако-додатний, то, очевидно, щоб дослідити, чи будь-який ряд 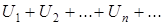 є абсолютно збіжним, ми можемо використовувати ознаки збіжності, виведені для знакододатних рядів, замінивши у відповідних виразах члени даного ряду їх абсолютними значеннями. Так, ознака Даламбера збіжності ряду запишеться тоді у вигляді
є абсолютно збіжним, ми можемо використовувати ознаки збіжності, виведені для знакододатних рядів, замінивши у відповідних виразах члени даного ряду їх абсолютними значеннями. Так, ознака Даламбера збіжності ряду запишеться тоді у вигляді 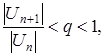 ознака Коші – у вигляді:
ознака Коші – у вигляді: 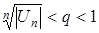 і т.п.
і т.п.
Означення. Якщо ряд 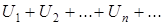 (*) збіжний, а ряд
(*) збіжний, а ряд 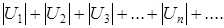 розбіжний, то даний ряд (*) називається умовно збіжним.
розбіжний, то даний ряд (*) називається умовно збіжним.
Отже, ряд 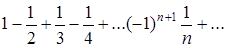
умовно збіжний,
Так само ряд 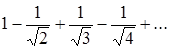
умовно збіжний, бо ряд
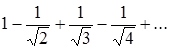 є ряд Діріхле-Рімана, в якому
є ряд Діріхле-Рімана, в якому 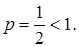
 2020-01-15
2020-01-15 222
222







