2020-01-15
96
План.
1. Означення знакочергуючого ряду.
2. Ознака Лейбніца.
3. Оцінка залишку знакочергуючого ряду, збіжного за ознакою Лейбніца.
Л-ра: Методичні вказівки до вивчення теми “Ряди”. Укладачі: В.О.Борисенко, В.В.Левчук, В.С.Мартиненко, В.Д.Подільчук. КДТЕУ. К, 1992 р. ст. 16-19.
Означення. Знакозмінними рядами називаються ряди виду:
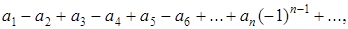
де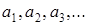 
- додатні числа.
Теорема Лейбніца. Якщо в знакозмінному ряді абсолютне значення загального члена монотонно прямує до нуля (тобто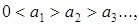 
до того ж 
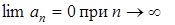), тоді знакозмінний ряд збігається, причому сума його має числове значення, проміжне між нулем та першим членом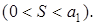 
Доведення. Розглянемо спочатку частинну суму парного порядку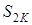 
, причому запишемо її в двох різних виглядах:
1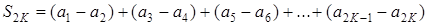 
.
Помічаємо, що чим більше К, тим більше пар, але кожна пара додатна, отже, 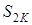монотонно зростає при збільшенні К.
2 З другого боку
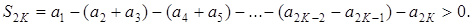
Бачимо, що <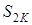 
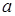, для всіх значень k > 1. Отже, 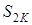обмежена зверху.
Зіставляючи обидва факти, приходимо до висновку, що величина 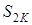монотонна і разом з тим обмежена змінна, том вона, прямує до певної скінченої границі 
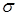, при чому ця границя, очевидно, більша за а 1 – а 2 і не перевищує а1:
а 1 – а 2 < 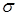< а 1.
Отже, напевне 0 < 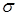< а 1.
Розглядаючи вже тепер частинну суму непарного порядку 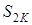+1, маємо:
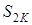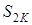= + а 2к+1.
Отже,
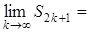
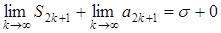
Остаточно приходимо до висновку, що існує єдина границя:
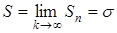(0 < S < a 1),
коли індекс n – будь-яке натуральне число як парне, так і непарне, що доводить теорему.
Наслідок. За умовою теореми Лейбніца остаточна S – Sn = rn менша за абсолютним значенням, ніж абсолютне значення першого з відкинутих членів:
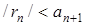, і має знак цього члена.
Доведення. Маємо:
,
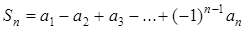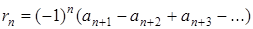
Ряд в останніх дужках сам по собі є знакозмінний і задовольняє теорему Лейбніца, тому
,
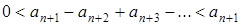причому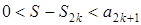 
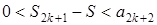
Отже, якщо перший з відкинутих членів непарний, то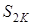 
представляє S з недостачею. Похибка має знак плюс. Якщо ж перший відкинутий член – парний, то 
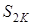, представляє S з надлишком. Похибка має знак мінус. В обох випадках, як бачимо, похибка має знак першого відкинутого члена і менша за абсолютним значенням, ніж абсолютне значення першого з відкинутих членів.
