Введение в алгоритмы

СОДЕРЖАНИЕ

Элементы дискретной математики. 4

1. Элементы теории множеств. 4

2. Бинарные отношения. 5

3. Логика высказываний. 6

4. Теория графов. 7

5. Введение в алгоритмы. 11

6. Основные алгебраические структуры. 13

7. Элементы теории формальных языков и автоматов. 14

Основы молекулярных вычислений и биоинформатики. 16

8. Основы молекулярных вычислений. 16

9. Применение молекулярных компьютеров в медицине. 17

10. Вычисления в живых клетках. 17

11. Системы Линденмайера. 18

Задания для самоконтроля. 19

Вопросы к зачету по курсу «Элементы дискретной математики и биоинформатики»: 24

Рекомендуемая литература. 27

 

Элементы дискретной математики.

Элементы теории множеств.

Лекция 1.

Понятие множества является одним из главных математических понятий, без которых невозможно изучение любого раздела математики. Такие понятия (множество, отношение, функция и др.) представляют собой основу математической культуры, которая является важной частью культуры общечеловеческой. Множество относится к математическим объектам, для которых нет строгого определения. Другим примером неопределяемого понятия служит точка в геометрии. Такие понятия вводятся на интуитивном уровне, но зато на их основе даются строгие определения других математических объектов. Можно сказать, что множество – это любая совокупность определенных и различимых между собой объектов, рассматриваемая как единое целое. Эти объекты называются элементами множества.

При изучении данного раздела, предполагается наличие у студентов представлений о понятии множества и операций над ними из курса высшей математики, поэтому главная установка здесь состоит в систематизации этих сведений. Особое внимание уделяется способам формального задания множеств, а также формальным определениям операций над множествами и их свойствам.

Краткое содержание раздела:

Понятие множества. Способы задания множеств. Диаграммы Эйлера-Венна. Подмножества. Равенство множеств. Множество всех подмножеств конечного множества. Пустое и универсальное множество. Примеры. Операции над множествами: пересечение, объединение, разность. Основные свойства операций объединения и пересечения: коммутативность, ассоциативность, дистрибутивность. Операция дополнения. Законы де Моргана. Мощность множества. Конечные и счетные множества.

Литература: [5] стр. 12-15, [16] гл.1, стр. 19-31.

Задачи: [6], №№ 101 (1, 3), 106 (1,3,5,7), 118, 128 (1,3,5,7), 139 (1,3,5).

Пример решения задач:

Найти множество всех подмножеств множества .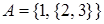

Решение. Множество A состоит из двух элементов, один из которых число 1, а второй – множество {2, 3}. Тогда множество всех подмножеств P(A) имеет 2²=4 элемента: .

 

Бинарные отношения.

Лекции 2-3.

Между элементами различных множеств могут быть установлены многочисленные связи и зависимости. Эти связи описываются в математике с помощью отношений и функций. Поскольку с понятием функции студенты знакомятся в курсе высшей математики в 1-м и 2-м семестрах, данный раздел посвящен понятию бинарного отношения и различным его свойствам. Отметим, что в биологии бинарные отношения могут использоваться для описания наследственных связей: например, отношение «быть предком» на множестве всех людей. Также важную роль при классификации играют отношения эквивалентности, например, эквивалентность «иметь одинаковое строение цветка, плода и одинаковый тип соцветия» на множестве всех цветковых растений делит их на классы эквивалентности – семейства – крестоцветных, розоцветных, бобовых и т.д.

В результате изучения данного раздела студенты должны усвоить понятие бинарного отношения, научиться интерпретировать отношения между реально существующими объектами формально, в терминах бинарных отношениях на множествах и их свойств.

Краткое содержание раздела:

Декартово произведение двух множеств. Понятие бинарного отношения. Примеры. Операции над отношениями, обращение, умножение. Свойства операций. Свойства отношений: рефлексивность, симметричность, транзитивность, антисимметричность, линейность. Примеры. Отношения эквивалентности и частичного порядка. Классы эквивалентности, фактор-множества. Связь отношения эквивалентности с разбиением множества. Отношение частичного порядка, отношение линейного порядка. Частично упорядоченные и линейно упорядоченные множества. Примеры.

Литература: [5] стр. 16-21, стр. 44-46, [16] гл. 2, стр. 32-39.

Задачи: [6] №№ 204 (1,5,9,14), 205 (1,3,5), 207 (1,3), 219, 303, 304.

Пример решения задач:

Пусть М – множество всех слов русского языка. Какими свойствами обладают отношения слова х и у не содержат ни одной общей буквы} и 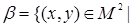слова х и у содержат хотя бы одну общую букву}. Будут ли эти отношения отношениями эквивалентности?

Решение. Рассмотрим сначала отношение . Ясно, что оно не является рефлексивным (поскольку у слов х и х все буквы общие, следовательно пара (х,х) не принадлежит ). Это отношение является симметричным, но не является транзитивным, поскольку, например, слова кот, пёс и слова пёс, мышка находятся в отношении , но слова кот, мышка не принадлежат этому отношению, поскольку имеют общую букву к. Следовательно, отношение  не является отношением эквивалентности.

Рассмотрим теперь отношение . Очевидно, что оно является рефлексивным и симметричным. Оно не транзитивно, поскольку, например, слова кот, компот и слова компот, мама принадлежат отношению , но слова кот, мама ему не принадлежат, т.к. не имеют общих букв.

 

Логика высказываний.

Лекция 4.

Математика развивается по своим внутренним законам, а именно, по законам логики. Математическая логика – это теория верных рассуждений. Слово «верных» не следует понимать в абсолютном смысле. Большинство естественнонаучных дисциплин строится на основе некоторых исходных договоренностей, или аксиом, принципов, которые формулируются исходя из разумных соображений здравого смысла или опыта. Далее из аксиом выводятся следствия, причем доказательство строится по законам логического вывода, которыми обеспечивает как раз математическая логика. Данный раздел посвящен основам математической логики, которую еще называют формальной логикой. Формальной, потому что она позволяет проверить правильность рассуждений, независимо от их содержания. Цепочки рассуждений в совершенно разных областях математики и других наук можно одинаково описать на языке логики и убедиться в их справедливости или ошибочности.

Цель данного раздела – способствовать выработке у студентов навыков строгих логически обоснованных методов рассуждений и доказательств.

Краткое содержание раздела:

Высказывания. Примеры. Логические связки. Формулы логики высказываний. Примеры. Логическая эквивалентность. Свойства логических операций. Тавтологии или законы логики высказываний. Логический вывод. Доказательство теорем.

Литература: [16] гл. 3, стр. 61-81, [5] стр. 65-85.

Задачи: [6] №№ 601 (1,4,7,10,13,16), 602 (1,3), 604 (1,3,5), 612 (1,3,4).

Пример решения задач:

В одной местности расположены два города И и Л. Жители И всегда говорят правду, а жители Л всегда лгут. Как, попав в один из этих городов, узнать у первого встречного название города?

Решение. Поскольку ответ встречного зависит от его правдивости, обозначим х =«Ты правдив». Нас интересует название города, поэтому обозначим у =«Это город И». Теперь из высказываний х и у сконструируем высказывание р так, что услышав от встречного ответ «Да» на вопрос «Верно ли, что р =И?» мы поймем, что находимся в И. Составим для р следующую таблицу истинности:

 

		Слышимый ответ	Понимаемый ответ	Р
Л	Л	нет	да	И
Л	И	да	нет	Л
И	Л	нет	нет	Л
И	И	да	Да	И

Таким образом, . В переводе на русский язык соответсвующий вопрос таков: «Верно ли, что ты лжец и это Л или ты правдив и это И?». Проще его можно сформулировать так: «Ты житель этого города?».

 

Теория графов.

Лекции 5-15.

Теория графов является, по сути, языком современной дискретной математики, в связи с бурным развитием компьютерной техники идеи и методы теории графов проникают во все новые области человеческого зна­­ния. Знакомство с основами теории графов и ее прикладными аспектами поможет студентам более успешно осваивать дисциплины, связанные с информатикой и некоторыми аспектами прикладной биологии. Так, например, деревья играют большую роль в биологической теории ветвящихся процессов.

Цель данного раздела – представить основное, устоявшееся ядро современной теории графов, акцентируя внимание на биологических приложениях. Для более полного охвата разделов современной теории графов, некоторые факты приводятся без доказательств (например, критерий планарности графа – теорема Понтрягина-Куратовского или теорема Хивуда о 5-раскрашиваемости планарного графа).

Краткое содержание раздела:

Способы формального задания графов. Степень вершины. Лемма о рукопожатиях. Подграфы, остовные подграфы. Полные графы. Число ребер полного графа. Подграфы, остовные подграфы. Пересечение и объединение подграфов.

Понятие маршрута на графе, виды маршрутов: цепи, циклы. Понятие связности графа. Представление произвольного графа в виде дизъюнктного объединения своих компонент связности. Разрезающие множества, мосты. Верхняя и нижняя границы для числа ребер в обыкновенном графе. Расстояния в графах, радиус и диаметр связного графа.

Ориентированные графы. Турниры. Ормаршруты, орцепи, орциклы (контуры). Орлемма о рукопожатиях.

Матрицы, ассоциированные с графами: матрица смежности, матрица инцидентности. Их свойства.

Понятие дерева, свойства деревьев. Понятие леса, свойства лесов. Применение деревьев в биологии для моделирования эволюционных процессов. Понятие остова, его свойства, цикломатическое число. Число остовов в обыкновенном связном графе. Число помеченных деревьев порядка n.

Эйлеровы графы, их свойства.

Гамильтоновы графы. Достаточное условие гамильтоновости графа (теорема Дирака).

Укладки графов. Планарные графы. Укладка графа в трехмерном пространстве. Эквивалентность планарности и укладываемости графа на сфере. Формула Эйлера для плоских графов. Связь числа вершин, ребер и граней выпуклых многогранников в трехмерном евклидовом пространстве. Непланарность графов К_3,3 и К₅. Теорема Понтрягина-Куратовского.

Раскраски графов. Хроматические числа. Теорема Кенига о 2-хроматичности обыкновенного графа. Теорема Хивуда о 5-раскрашиваемости любого планарного графа.

Литература: [1] гл. 1-3, 5-6, [7].

Задачи: [12] №№ 1, 4, 17, 18, 19, 37, 38, 39, 46, 54, 55, 56, 58, 59, 60, 63, 64, 74, 77, 94, 95.

Пример решения задач:

5.1. В соревновании по круговой системе с двенадцатью участниками провели все встречи. Сколько встреч было сыграно?

Решение. Построим граф встреч игроков: каждому из 12-ти игроков поставим в соответствие вершину графа. Если два игрока встретились между собой, то соединим соответствующие вершины ребром. Поскольку соревнование проводится по круговой системе, т.е. каждый играет с каждым, и были сыграны все встречи, то граф встреч является полным графом на 12-ти вершинах. Число ребер в нем . Таким образом, было сыграно 66 встреч.

 

5.2. Рассмотрим граф 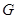, изображенный на рисунке. На примере этого графа рассмотрим некоторые понятия теории графов.

Степенью (валентностью) вершины  неориентированного графа  называется число ребер , инцидентных данной вершине. Таблица степеней вершин данного графа имеет вид:

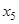
	3	3	3	4	2	3	2

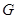Матрицей смежности неориентированного графа  называется матрица размерности , элементы которой определяются следующим образом:

Матрица смежности для данного графа имеет вид:

.

Матрицей инцидентности неориентированного графа  с  вершинами и  ребрами называется матрица размерности , элементы которой определяются следующим образом:

В графе  обозначим ребро, соединяющее вершины  и 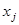, через  (два индекса использовать удобнее). Так, например, ребро 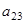 инцидентно вершинам  и . Матрица инцидентности для нашего графа имеет вид:

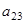
		1	1	1	0	0	0	0	0	0	0
		1	0	0	1	1	0	0	0	0	0
		0	0	0	1	0	1	1	0	0	0
		0	1	0	0	1	1	0	1	0	0
		0	0	1	0	0	0	0	0	1	0
		0	0	0	0	0	0	0	1	1	1
		0	0	0	0	0	0	1	0	0	1

Обозначения вершин и ребер графа не включаются в матрицу инцидентности, а записаны только для удобства.

Расстоянием  между вершинами  и  в неориентированном графе  называется наименьшее число ребер, соединяющих эти вершины. Условный радиус графа  относительно вершины 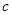 определяется формулой:

. Здесь  – это множество вершин графа .

Радиус графа G определяется как наименьший из условных радиусов графа, а центр графа составляют вершины, условные радиусы графа относительно которых совпадают с радиусом графа.

Для данного графа таблица расстояний и условных радиусов вершин имеет вид:

	0	1	2	1	1	2	3	3
	1	0	1	1	2	2	2	2
	2	1	0	1	3	2	1	3
	1	1	1	0	2	1	2	2
	1	2	3	2	0	1	2	3
	2	2	2	1	1	0	1	2
	3	2	1	2	2	1	0	3

Радиус графа 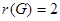, следовательно, центр графа – это множество вершин .

5.3. Из одной бактерии в результате деления получилось 1000 бактерий: вначале бактерия разделилась на две, затем одна из них вновь разделилась на две, затем одна из трех бактерий разделилась на две и т.д. Докажите, что в некоторый момент существовала бактерия, число потомков которой в самом конце, т.е. среди 1000 бактерий не меньше 100 и не больше 199.

Решение. Процесс деления бактерий опишем корневым деревом. Условимся называть дочками бактерии те две бактерии, на которые она разделилась. Обозначим через Б₁, Б₂, Б₃, … такую последовательность бактерий:

Б₁ – исходная бактерия, число ее потомков П₁=1000;

Б₂ – та из дочек Б₁, у которой число потомков не меньше, чем у другой дочки бактерии Б₁;

Б₃ – та из дочек Б₂, у которой число потомков не меньше, чем у другой дочки бактерии Б₂ и т.д.

В силу выбора нами дочерних бактерий следует, что .

Последовательность натуральных чисел П₁, П₂, П₃, … монотонно убывает. Первый член этой последовательности равен 1000, последний – 2. Значит, найдется такой номер k, когда число П_k в первый раз станет меньше 200, т.е. когда  и . Учитывая, что , получим , т.е. число потомков бактерии Б_k не меньше 100 и не больше 199.

 

Введение в алгоритмы.

Лекции 16-17.

Цель данного раздела – дать общее представление о теории алгоритмов, обсудить вопросы сложности и эффективности, рассмотреть классические примеры алгоритмов на графах, а также примеры биологических задач, использующих алгоритмические методы решения. Тем самым, этот раздел с одной стороны позволяет студентам более успешно осваивать дисциплины, связанные с информатикой, с другой стороны дает предварительные сведения из теории алгоритмов, необходимые при изучении второй части курса, посвященной основам биоинформатики. 

В качестве примера, приведем две типичные задачи биоинформатики. Первая задача – задача сравнения последовательностей. Дана аминокислотная последовательность, похожая на некоторую другую последовательность, хранящуюся в банке данных, т.е. по которой имеются экспериментальные данные, и известны ее функции. Тогда можно предположить, что эти последовательности выполняют сходные функции. Таким образом, после секвенирования новой последовательности ее сравнивают с уже существующими в базах данных последовательностями, чтобы судить о том, какие функции несет эта последовательность. Следовательно, возникает задача поиска сходства последовательностей, а именно: одна последовательность записывается под другой, и требуется найти наилучший вариант так выровнять эту пару последовательностей, чтобы количество совпадений было максимальным. Качество выравнивания оценивают, назначая штрафы за несовпадение букв и за наличие пробелов (когда приходится раздвигать одну последовательность для того, чтобы получить наибольшее число совпадающих позиций). Ясно, что можно найти оптимальное выравнивание перебором всех возможных вариантов, но на практике этот способ неприменим – число возможных выравниваний экспоненциально зависит от длины последовательности. Тем не менее, для решения этой задачи существует эффективный алгоритм: она сводится к задаче поиска кратчайшего пути во взвешенном графе.

Другая задача – предсказание вторичной структуры РНК. Вторичная структура РНК – структура, образуемая спаренными основаниями на однонитевой молекуле РНК. Вся РНК состоит из петель и спиралей. Петли бывают следующих типов: шпилька, внутренняя, выпячивание, множественная, псевдоузел. Таким образом, задача определения вторичной структуры состоит в правильном определении спаренных нуклеотидов. Эту задачу можно интерпретировать в терминах теории графов: «правильной» вторичной структуре будет соответствовать максимальный подграф (клика) в графе потенциальных спиралей. Однако известно, что задача поиска клики в графе является труднорешаемой – для нее, скорее всего, не существует более эффективного алгоритма решения, чем полный перебор всех вариантов. Тем не менее, на практике эта задача решается приближенно, используя алгоритм динамического программирования.

Краткое содержание раздела:

Понятие алгоритма. Алгоритмы и их сложность. Полиномиальные и экспоненциальные алгоритмы. Эффективные и неэффективные алгоритмы. Примеры задач: задача о кратчайшем пути во взвешенном графе, задача о минимальном остове. Алгоритм Краскала. Труднорешаемые задачи: задача коммивояжера, задача о максимальном полном подграфе. Поиск в графе: поиск в глубину, поиск в ширину. Поиск кратчайшего по числу ребер пути. Алгоритм отыскания эйлеровой цепи в эйлеровом графе. Некоторые типичные задачи биоинформатики, сводящиеся к задачам на графах: задача сравнения последовательностей, задача предсказания вторичной структуры РНК, задача поиска кратчайшей надстроки, расшифровка гибридизацией.

Литература: [1], гл. 7 стр. 207-213, гл. 8 стр. 226-232, 247-262.

Задачи: [12] №№ 59, 61.