2020-01-15
295
Решётка L называется дистрибутивной, если для любых 
выполняется:
D1. 
.
D2.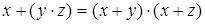 
.
В любой решётке тождества D1 и D2 равносильны. Доказательство этого факта содержится в книге [2], стр. 24.
Примеры дистрибутивных решёток:
1. Множество целых положительных чисел, 
означает, что 
делит 
. Это решётка с операциями НОД и НОК.
2. Любая цепь является дистрибутивной решёткой.
 |
ТЕОРЕМА 1.2. Решётка L с 0 и 1 является дистрибутивной тогда и только тогда, когда она не содержит подрешёток вида
Доказательство этой теоремы можно найти в книге [1].
