Всюду далее под словом «решётка» понимается произвольная дистрибутивная решётка с 0.
Решётка L называется обобщённой булевой, если для любых элементов  и d из L, таких что
и d из L, таких что  существует относительное дополнение на интервале
существует относительное дополнение на интервале  , т.е. такой элемент
, т.е. такой элемент 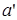 из L, что
из L, что  и
и  .
.
(Для 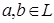 ,
, 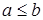 , интервал
, интервал  |
|  ; для
; для  ,
, 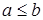 можно так же определить полуоткрытый интервал
можно так же определить полуоткрытый интервал  |
|  ).
).
ТЕОРЕМА 1.3. (О единственности относительного дополнения в обобщённо булевой решётке). Каждый элемент обобщённо булевой решётки L имеет только одно относительное дополнение на промежутке.
Доказательство. Пусть для элемента  существует два относительных дополнения
существует два относительных дополнения  и
и  на интервале
на интервале  . Покажем, что
. Покажем, что  . Так как
. Так как  относительное дополнение элемента
относительное дополнение элемента  на промежутке
на промежутке  , то
, то  и
и  , так же
, так же  относительное дополнение элемента
относительное дополнение элемента  на промежутке
на промежутке  , то
, то  и
и 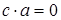 .
.
Отсюда
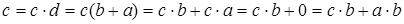
 ,
,
таким образом  , т.е. любой элемент обобщённой булевой решётки имеет на промежутке только одно относительное дополнение.
, т.е. любой элемент обобщённой булевой решётки имеет на промежутке только одно относительное дополнение.
Решётка L называется булевой, если для любого элемента  из L существует дополнение, т.е. такой элемент
из L существует дополнение, т.е. такой элемент 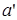 из L, что
из L, что  и
и 
ТЕОРЕМА 1.4. (О единственности дополнения в булевой решётке). Каждый элемент булевой решётки L имеет только одно дополнение.
Доказательство аналогично доказательству теоремы 1.3.
ТЕОРЕМА 1.5. (О связи обобщённо булевых и булевых решёток).
Любая булева решётка является обобщённо булевой, обратное утверждение не верно.
Доказательство. Действительно, рассмотрим произвольную булеву решётку L. Возьмём элементы a и d из L, такие что 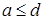 . Заметим, что относительным дополнением элемента a до элемента d является элемент
. Заметим, что относительным дополнением элемента a до элемента d является элемент  , где a’ – дополнение элемента a в булевой решётке L. Действительно,
, где a’ – дополнение элемента a в булевой решётке L. Действительно,  , кроме того
, кроме того  . Отсюда следует, что решётка L является обобщённо булевой.
. Отсюда следует, что решётка L является обобщённо булевой.
Идеалы
Подрешётка I решётки L называется идеалом, если для любых элементов  и
и  элемент
элемент  лежит в I. Идеал I называется собственным, если
лежит в I. Идеал I называется собственным, если  . Собственный идеал решётки L называется простым, если из того, что
. Собственный идеал решётки L называется простым, если из того, что  и
и  следует
следует  или
или  .
.
Так как непустое пересечение любого числа идеалов снова будет идеалом, то мы можем определить идеал, порождённый множеством H в решётке L, предполагая, что H не совпадает с пустым множеством. Идеал, порождённый множеством H будет обозначаться через (H]. Если 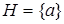 , то вместо
, то вместо  будем писать
будем писать  и называть
и называть  главным идеалом.
главным идеалом.
ТЕОРЕМА 1.5. Пусть L – решётка, а H и I – непустые подмножества в L, тогда I является идеалом тогда и только тогда, когда если  , то
, то  , и если
, и если  , то
, то  .
.
Доказательство. Пусть I – идеал, тогда  влечёт за собой
влечёт за собой  , так как I – подрешётка. Если
, так как I – подрешётка. Если 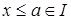 , то
, то 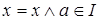 и условия теоремы проверены.
и условия теоремы проверены.
Обратно, пусть I удовлетворяет этим условиям и  . Тогда
. Тогда  и так как
и так как  , то
, то  , следовательно, I – подрешётка. Наконец, если
, следовательно, I – подрешётка. Наконец, если 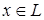 и
и  , то
, то 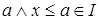 , значит,
, значит,  и I является идеалом.
и I является идеалом.
Глава 2
Конгруэнции
Отношение эквивалентности (т.е. рефлексивное, симметричное и транзитивное бинарное отношение)  на решётке L называется конгруэнцией на L, если
на решётке L называется конгруэнцией на L, если  и
и  совместно влекут за собой
совместно влекут за собой  и
и  (свойство стабильности). Простейшими примерами являются ω, ι, определённые так:
(свойство стабильности). Простейшими примерами являются ω, ι, определённые так:
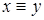 (ω)
(ω) 
 ;
; 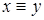 (ι) для всех
(ι) для всех  .
.
Для  обозначим через
обозначим через  смежный класс, содержащий элемент
смежный класс, содержащий элемент  , т.е.
, т.е. 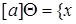 |
| 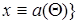
Пусть L – произвольная решётка и  . Наименьшую конгруэнцию, такую, что
. Наименьшую конгруэнцию, такую, что  для всех
для всех 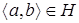 , обозначим через
, обозначим через  и назовём конгруэнцией, порождённой множеством
и назовём конгруэнцией, порождённой множеством 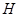 .
.
ЛЕММА 2.1. Конгруэнция  существует для любого
существует для любого  .
.
Доказательство. Действительно, пусть Ф = 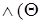 |
|  для всех
для всех 
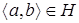 . Так как пересечение в решётке
. Так как пересечение в решётке  совпадает с теоретико-множественным пересечением, то
совпадает с теоретико-множественным пересечением, то  для всех
для всех 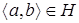 . Следовательно, Ф =
. Следовательно, Ф =  .
.
В двух случаях мы будем использовать специальные обозначения: если  или
или  и
и  - идеал, то вместо
- идеал, то вместо  мы пишем
мы пишем  или
или  соответственно. Конгруэнция вида
соответственно. Конгруэнция вида 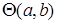 называется главной; её значение объясняется следующей леммой:
называется главной; её значение объясняется следующей леммой:
ЛЕММА 2.2.  =
= 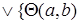 |
|  .
.
Доказательство. Пусть 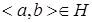 , тогда
, тогда 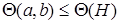 , отсюда
, отсюда  . С другой стороны рассмотрим
. С другой стороны рассмотрим  , но тогда
, но тогда  . Поэтому
. Поэтому 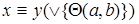 и
и  .
.
Заметим, что 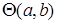 - наименьшая конгруэнция, относительно которой
- наименьшая конгруэнция, относительно которой  , тогда как
, тогда как  - наименьшая конгруэнция, такая, что
- наименьшая конгруэнция, такая, что  содержится в одном смежном классе. Для произвольных решёток о конгруэнции
содержится в одном смежном классе. Для произвольных решёток о конгруэнции  почти ничего не известно. Для дистрибутивных решёток важным является следующее описание конгруэнции
почти ничего не известно. Для дистрибутивных решёток важным является следующее описание конгруэнции 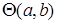 :
:
ТЕОРЕМА 2.1. Пусть  - дистрибутивная решётка,
- дистрибутивная решётка,  и
и 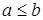 . Тогда
. Тогда  и
и  .
.
Доказательство. Обозначим через Ф бинарное отношение, определённое следующим образом:  и
и  .
.
Покажем, что Ф – отношение эквивалентности:
1) Ф – отношение рефлексивности: x·a = x·a; x+b = x+b;
2) Ф – отношение симметричности:

 x·a = y·a и x+b = y+b
x·a = y·a и x+b = y+b  y·a = x·a и y+b = x+b
y·a = x·a и y+b = x+b 
 ;
;
3) Ф – отношение транзитивности.
Пусть 
 x ·a = y·a и x+b = y+b и пусть
x ·a = y·a и x+b = y+b и пусть 
 y·с = z·с и y+d = z+d. Умножим обе части x·a = y·a на элемент с, получим x·a·c = y·a·c. А обе части y·с = z·с умножим на элемент a, получим y·c·a = z·c·a. В силу симметричности x·a·c = y·a·c = z·a·c. Аналогично получаем x+b+d = y+b+d = z+b+d. Таким образом
y·с = z·с и y+d = z+d. Умножим обе части x·a = y·a на элемент с, получим x·a·c = y·a·c. А обе части y·с = z·с умножим на элемент a, получим y·c·a = z·c·a. В силу симметричности x·a·c = y·a·c = z·a·c. Аналогично получаем x+b+d = y+b+d = z+b+d. Таким образом  .
.
Из всего выше обозначенного следует, что Ф – отношение эквивалентности.
Покажем, что Ф сохраняет операции. Если  и z
и z  L, то (x+z) ·a = (x·a) + (z·a) = (y·a) + (z·a) = (y+z) ·a и (x+z)+b = z+(x+b) = z+(y+b); следовательно,
L, то (x+z) ·a = (x·a) + (z·a) = (y·a) + (z·a) = (y+z) ·a и (x+z)+b = z+(x+b) = z+(y+b); следовательно,  . Аналогично доказывается, что
. Аналогично доказывается, что  и, таким образом, Ф – конгруэнция.
и, таким образом, Ф – конгруэнция.
Наконец, пусть  - произвольная конгруэнция, такая, что
- произвольная конгруэнция, такая, что  , и пусть
, и пусть  . Тогда x·a = y·a, x+b = y+b,
. Тогда x·a = y·a, x+b = y+b,  и
и  . Поэтому вычисляя по модулю
. Поэтому вычисляя по модулю  , получим
, получим

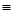
 , т.е.
, т.е.  , и таким образом,
, и таким образом,  .
.
СЛЕДСТВИЕ ИЗ ТЕОРЕМЫ 2.1. Пусть I – произвольный идеал дистрибутивной решётки L. Тогда  в том и только том случае, когда
в том и только том случае, когда 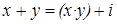 для некоторого
для некоторого  . В частности, идеал I является смежным классом по модулю
. В частности, идеал I является смежным классом по модулю  .
.
Доказательство. Если  , то
, то  и элементы x·y·i, i принадлежат идеалу I.
и элементы x·y·i, i принадлежат идеалу I.
Действительно  .
.
Покажем, что  .
.
Воспользуемся тем, что  (*), заметим, что
(*), заметим, что 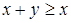 и
и  , поэтому мы можем прибавить к тождеству (*)
, поэтому мы можем прибавить к тождеству (*)  или
или  , и тождество при этом будет выполняться.
, и тождество при этом будет выполняться.
 Прибавим
Прибавим  :
:  , получим
, получим  .
.
 Прибавим
Прибавим  :
:  , получим
, получим 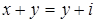 .
.
Отсюда  . Таким образом,
. Таким образом,  .
.
Обратно согласно лемме 2,  |
| 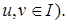
Однако  и поэтому
и поэтому  |
| 
Если  , то
, то  откуда
откуда
 .
.
Действительно,  (**).
(**).
Рассмотрим правую часть этого тождества:
Объединим первое и второе слагаемые –
 .
.
Объединим первое и третье слагаемые –
 ,
,
таким образом  (***)
(***)
Заметим, что  , поэтому прибавим к обеим частям выражения (***) y:
, поэтому прибавим к обеим частям выражения (***) y:


Но 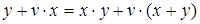 , отсюда
, отсюда  .
.
Следовательно, условие следствия из теоремы 2.1. выполнено для элемента 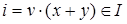 . Наконец, если
. Наконец, если  и
и  , то
, то  , откуда
, откуда  и
и  , т.е.
, т.е.  является смежным классом.
является смежным классом.
ТЕОРЕМА 2.2. Пусть L – булева решётка. Тогда отображение 
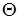
 является взаимно однозначным соответствием между конгруэнциями и идеалами решётки L. (Под
является взаимно однозначным соответствием между конгруэнциями и идеалами решётки L. (Под 
 понимаем класс нуля по конгруэнции
понимаем класс нуля по конгруэнции  , под
, под  понимаем решётку конгруэнций.)
понимаем решётку конгруэнций.)
 Доказательство. В силу следствия из теоремы 2.1. это отображение на множество идеалов; таким образом мы должны только доказать, что оно взаимно однозначно, т.е. что смежный класс
Доказательство. В силу следствия из теоремы 2.1. это отображение на множество идеалов; таким образом мы должны только доказать, что оно взаимно однозначно, т.е. что смежный класс  определяет конгруэнцию
определяет конгруэнцию  . Это утверждение, однако, очевидно. Действительно
. Это утверждение, однако, очевидно. Действительно  тогда и только тогда, когда
тогда и только тогда, когда  (*), последнее сравнение в свою очередь равносильно сравнению
(*), последнее сравнение в свою очередь равносильно сравнению  , где с – относительное дополнение элемента
, где с – относительное дополнение элемента  в интервале
в интервале 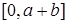 .
.
Действительно, помножим выражение (*) на с:
 , но
, но 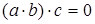 , а
, а 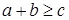 , отсюда
, отсюда  .
.
Таким образом, 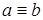 в том и только том случае, когда
в том и только том случае, когда  .
.
Примечание. Приведённое доказательство не полностью использует условие, что L – дистрибутивная решётка с дополнениями. Фактически, мы пользовались только тем, что L имеет нуль и является решёткой с относительными дополнениями. Такая решётка называется обобщённой булевой решёткой.
ТЕОРЕМА 2.3 (Хасимото [1952]). Пусть L – произвольная решётка. Для того, чтобы существовало взаимно однозначное соответствие между идеалами и конгруэнциями решётки L, при котором идеал, соответствующий конгруэнции  , являлся бы смежным классом по
, являлся бы смежным классом по  , необходимо и достаточно, чтобы решётка L была обобщённой булевой.
, необходимо и достаточно, чтобы решётка L была обобщённой булевой.
 Доказательство. Достаточность следует из доказательства теоремы 2.2. Перейдём к доказательству необходимости.
Доказательство. Достаточность следует из доказательства теоремы 2.2. Перейдём к доказательству необходимости.
Идеалом, соответствующим конгруэнции  , должен быть (0]; следовательно, L имеет нуль 0.
, должен быть (0]; следовательно, L имеет нуль 0.
 Если L содержит диамант
Если L содержит диамант  , то идеал (a] не может быть смежным классом, потому что из
, то идеал (a] не может быть смежным классом, потому что из  следует
следует  и
и 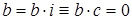 . Но
. Но 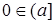 , значит, любой смежный класс, содержащий
, значит, любой смежный класс, содержащий  , содержит и
, содержит и  , и
, и  .
.
Аналогично, если L содержит пентагон  и смежный класс содержит идеал
и смежный класс содержит идеал 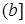 , то
, то  и
и  , откуда
, откуда  . Следовательно, этот смежный класс должен содержать
. Следовательно, этот смежный класс должен содержать  и
и  .
.
Итак, решётка L не содержит подрешёток, изоморфных ни диаманту, ни пентагону. Поэтому, по теореме 1.2., она дистрибутивна.
Пусть  и
и  . Согласно следствию из теоремы 2.1., для конгруэнции
. Согласно следствию из теоремы 2.1., для конгруэнции  идеал
идеал  так же является смежным классом, следовательно,
так же является смежным классом, следовательно,  , откуда
, откуда  . Опять применяя следствие из теоремы 2.1. получим,
. Опять применяя следствие из теоремы 2.1. получим, 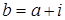 для некоторого
для некоторого  . Так как
. Так как  , то
, то  и
и  . Следовательно,
. Следовательно,  о полу орого ледствие 4 получим, цииодержать, соответствующим конгруэнции образом мы должны только доказать, ______________ и
о полу орого ледствие 4 получим, цииодержать, соответствующим конгруэнции образом мы должны только доказать, ______________ и 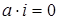 , т.е. элемент
, т.е. элемент  является относительным дополнением элемента
является относительным дополнением элемента  в интервале
в интервале  .
.
Основная теорема
(1)  Пусть
Пусть  - обобщённая булева решётка. Определим бинарные операции
- обобщённая булева решётка. Определим бинарные операции 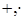 на B, полагая
на B, полагая  и обозначая через
и обозначая через 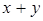 относительное дополнение элемента
относительное дополнение элемента  в интервале
в интервале  . Тогда
. Тогда 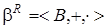 - булево кольцо, т.е. (ассоциативное) кольцо, удовлетворяющее тождеству
- булево кольцо, т.е. (ассоциативное) кольцо, удовлетворяющее тождеству  (а следовательно и тождествам
(а следовательно и тождествам  ,
,  ).
).
(2) Пусть  - булево кольцо. Определим бинарные операции
- булево кольцо. Определим бинарные операции  и
и  на
на 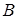 , полагая, что
, полагая, что  и
и  . Тогда
. Тогда  - обобщённая булева решётка.
- обобщённая булева решётка.
Доказательство.
(1) Покажем, что  - кольцо.
- кольцо.
Напомним определение. Кольцо  - это непустое множество
- это непустое множество 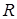 с заданными на нём двумя бинарными операциями
с заданными на нём двумя бинарными операциями 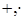 , которые удовлетворяют следующим аксиомам:
, которые удовлетворяют следующим аксиомам:
1. Коммутативность сложения:  выполняется
выполняется  ;
;
2. Ассоциативность сложения:  выполняется
выполняется  ;
;
3. Существование нуля, т.е.  ,
, 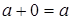 ;
;
4. Существование противоположного элемента, т.е. 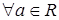 ,
,  ,
,  ;
;
5. Ассоциативность умножения:  ,
,  ;
;
6. Закон дистрибутивности.
Проверим, выполняются ли аксиомы кольца:
1. Относительным дополнением до  элемента
элемента  будет элемент
будет элемент  , а относительным дополнением
, а относительным дополнением 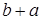 элемент
элемент 
 . В силу того, что
. В силу того, что  , а так же единственности дополнения имеем
, а так же единственности дополнения имеем  .
.
2. Покажем, что 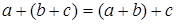 .
.
 Рассмотрим все возможные группы вариантов:
Рассмотрим все возможные группы вариантов:
1) Пусть 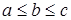 , тогда
, тогда  (Далее везде под элементом x будем понимать сумму
(Далее везде под элементом x будем понимать сумму  ).
).
Аналогично получаем 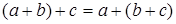 в случаях
в случаях  ,
,  ,
, 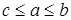 ,
,  и
и  . Заметим, что когда один из элементов равен нулю (например, c), то получаем тривиальные варианты (a+b=a+b).
. Заметим, что когда один из элементов равен нулю (например, c), то получаем тривиальные варианты (a+b=a+b).
2) Пусть 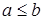 , а элемент c не сравним с ними. Возможны следующие варианты:
, а элемент c не сравним с ними. Возможны следующие варианты:



Нетрудно заметить, что во всех этих случаях  , кроме того:
, кроме того:
если c=a+b, то (a+b)+c=0=a+(b+c);
если c=0, то получаем тривиальный вариант.
Вариант, когда c равен наибольшему элементу решётки d, мы уже рассматривали.
Если c=b, то (a+b)+c=(a+b)+b=a и a+(b+c)=a+(b+b)=a.
Если c=a, то (a+b)+c=(a+b)+a=b и a+(b+c)=a+(b+a)=b.
 Аналогично для случаев
Аналогично для случаев  ,
,  ,
,  ,
, 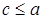 и
и 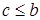 .
.
3) Под элементами нижнего уровня будем понимать элементы 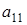 ,
,  ,
, 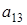 ,
,  ,
, 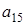 ,
,  ,
,  ,
,  , т.е. те элементы 4-х мерного куба, которые образуют нижний трёхмерный куб.
, т.е. те элементы 4-х мерного куба, которые образуют нижний трёхмерный куб.
Под элементами верхнего уровня будем понимать элементы 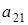 ,
, 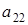 ,
,  ,
, 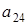 ,
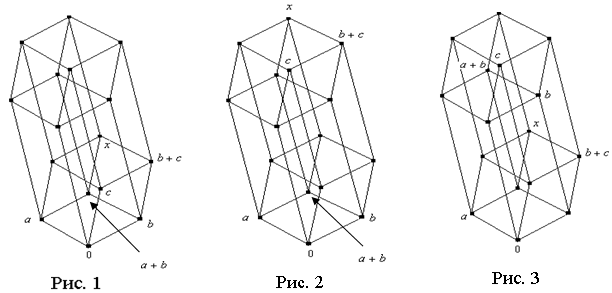
, 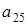 ,
,  ,
,  ,
, 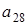 , т.е. те элементы 4-х мерного куба, которые образуют верхний трёхмерный куб.
, т.е. те элементы 4-х мерного куба, которые образуют верхний трёхмерный куб.
Под фразой «элемент верхнего уровня, полученный из элемента  нижнего уровня сдвигом по соответствующему ребру» будем понимать элемент
нижнего уровня сдвигом по соответствующему ребру» будем понимать элемент  верхнего уровня.
верхнего уровня.
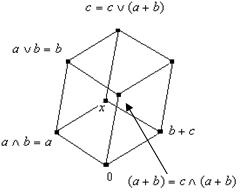
Пусть a, b, c несравнимы. Рассмотрим следующие варианты:  и
и 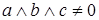 .
.
 Пусть
Пусть  . Заметим, что это возможно только в случаях, когда
. Заметим, что это возможно только в случаях, когда 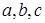 принадлежат нижнему уровню, причём лежат на позициях элементов
принадлежат нижнему уровню, причём лежат на позициях элементов  (рис. 1). Либо a, b остаются на своих позициях, элемент c сдвигается на верхний уровень по соответствующему ребру (рис. 2). Либо элемент a остаётся на своей позиции, элементы b, c сдвигаются на верхний уровень по соответствующему ребру (рис 3).
(рис. 1). Либо a, b остаются на своих позициях, элемент c сдвигается на верхний уровень по соответствующему ребру (рис. 2). Либо элемент a остаётся на своей позиции, элементы b, c сдвигаются на верхний уровень по соответствующему ребру (рис 3).
 Нетрудно заметить, что во всех этих случаях
Нетрудно заметить, что во всех этих случаях  .
.
Пусть  , здесь так же
, здесь так же  .
.
Таким образом мы рассмотрели все основные группы вариантов расположения элементов a, b, c и во всех этих случаях ассоциативность сложения выполняется.
3. Рассмотрим в решётке элемент 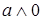 , к нему существует относительное дополнение
, к нему существует относительное дополнение  до элемента
до элемента  , т.е.
, т.е.  и
и 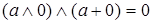 . Учитывая, что в решётке
. Учитывая, что в решётке  и
и  , имеем следующее:
, имеем следующее: 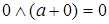 и
и  . Отсюда
. Отсюда  .
.
4. Рассмотрим относительное дополнение элемента  до
до  , это элемент
, это элемент 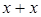 . Таким образом:
. Таким образом:  и
и  . Учитывая, что в решётке выполняются тождества
. Учитывая, что в решётке выполняются тождества  и
и  имеем следующее:
имеем следующее:  и
и  . Отсюда
. Отсюда 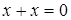 .
.
5. Так как в решётке выполняется ассоциативность  , а так же имея
, а так же имея  , то
, то  .
.
6. Докажем дистрибутивность 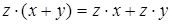 или что то же самое
или что то же самое
 (*).
(*).
Докажем, что дополнения левой и правой частей выражения (*) до верхней грани  совпадают.
совпадают.
Нетрудно заметить, что дополнением правой части выражения (*) до элемента  будет являться элемент
будет являться элемент  .
.
Покажем это:
 , по определению относительного дополнения элемента
, по определению относительного дополнения элемента  (
(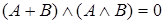 ), где за
), где за  приняли элемент
приняли элемент  , а элемент
, а элемент  за
за  .
.
 , по определению относительного дополнения элемента
, по определению относительного дополнения элемента  (
(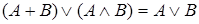 ), где за
), где за  приняли элемент
приняли элемент  , а элемент
, а элемент  за
за  .
.
Покажем, что и для левой части (*) элемент  будет являться относительным дополнением до верхней грани
будет являться относительным дополнением до верхней грани  :
:
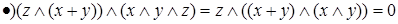 , т.к.
, т.к.  .
.

Мы показали, что дополнения элементов  и
и  до верхней грани
до верхней грани  совпадают, следовательно, в силу единственности дополнения
совпадают, следовательно, в силу единственности дополнения  . А значит и
. А значит и  , т.е. дистрибутивность доказана.
, т.е. дистрибутивность доказана.
Таким образом, для  все аксиомы кольца выполняются.
все аксиомы кольца выполняются.
Заметим, что  выполняется в силу того, что
выполняется в силу того, что  , а в решётке
, а в решётке  .
.
Также выполняется  , потому что
, потому что 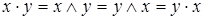 .
.
Таким образом,  - булево кольцо.
- булево кольцо.
Доказательство (2). Частичную упорядоченность  имеем исходя из того, что исходное булево кольцо
имеем исходя из того, что исходное булево кольцо 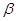 - частично упорядоченное множество. Кроме того
- частично упорядоченное множество. Кроме того 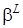 - решётка, т.к.
- решётка, т.к.  существуют sup(x,y) и inf(x,y), заданные соответствующими правилами:
существуют sup(x,y) и inf(x,y), заданные соответствующими правилами:  и
и  .
.
Покажем, что решётка дистрибутивна, т.е. что выполняется тождество  (*)
(*)
Рассмотрим левую часть выражения (*):
 .
.
Рассмотрим правую часть выражения (*):
 ,
,
т.о. тождество  верно, т.е. решётка
верно, т.е. решётка  является дистрибутивной.
является дистрибутивной.
Покажем, что у каждого элемента  в дистрибутивной решётке
в дистрибутивной решётке  есть относительное дополнение. Для этого рассмотрим произвольные элементы
есть относительное дополнение. Для этого рассмотрим произвольные элементы  , но они так же должны являться элементами решётки
, но они так же должны являться элементами решётки  , следовательно, в ней должны лежать и
, следовательно, в ней должны лежать и  , которым в кольце соответствуют
, которым в кольце соответствуют  .
.
Рассмотрим элемент булева кольца  (в решётке лежит соответствующий ему элемент), заметим, что
(в решётке лежит соответствующий ему элемент), заметим, что
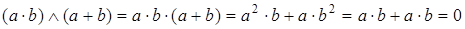
и  .
.
Поэтому элемент 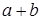 будет являться в дистрибутивной решётке
будет являться в дистрибутивной решётке 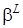 относительным дополнением
относительным дополнением  до верхней грани
до верхней грани 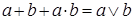 .
.
Таким образом,  будет являться дистрибутивной решёткой с относительными дополнениями (обобщённой булевой).
будет являться дистрибутивной решёткой с относительными дополнениями (обобщённой булевой).
 2020-01-15
2020-01-15 610
610