Значение эффективных численных методов минимизации функции одной переменной определяется в основном тем, что они входят составной частью во многие методы решения сложных экстремальных задач.
Существует множество различных методов нахождения экстремума функции. Отличаются они по скорости сходимости (количестве итераций необходимых для нахождения оптимума), количестве элементарных действий (необходимо или нет вычислять дополнительные функции, например, производные). Но сказать какой метод лучше или хуже можно только с натяжкой, т.к. это зависит от вида функций, например, метод чисел Фибоначчи считается самым быстрым из одномерных, однако он справедлив только для унимодальных функций. Метод локализации очень зависим от выбора начальной точки и приращения, но он способен локализовать экстремум в отличии от чисел Фибоначчи или "золотого сечения". Методы первого порядка просты в реализации. Для методов второго порядка требуется вычисление вторых производных, что в прикладных задачах или невозможно или сопряжено с большими затратами. Однако такие общие данные не могут служить основанием для оценки качества методов при решении конкретных задач. До настоящего времени нет достаточно обоснованных правил выбора методов решения.
Основной теории сходимости вычислительных методов служит теория устойчивости дискретных систем. В рамках этой теории сходимость многих модификаций (например, методов ньютоновского типа, квазиньютонофского методов первого и нулевого порядка) можно трактовать как сохранение свойства устойчивости при возмущении дискретных систем.
Важной особенность является то, что почти все эти методы находят локальный минимум на каком-либо отрезке, глобальный можно найти только методом перебора или аналитически, при реализации с помощью вычислительной техники второй способ не подходит.
Выбор метода для минимизации конкретной функции зависит от многих причин. Общая рекомендация состоит в том, что первые итерации строить методами нулевого или первого порядка, а затем в случае необходимости перейти к методам второго порядка. Метод сопряженных градиентов, будучи методом первого порядка, по объему итераций на итераций мало отличается от градиентных методов, но обладает сверхлинейной сходимостью. Следует однако, отметить его большую чувствительность к ошибкам округления. Методы второго порядка накладывают ограничение на функцию, необходимо чтобы она была дважды диффиринцируема и эта производная была положительна. Поэтому для нахождения минимума реализуем метод двумерной оптимизации - покоординатным спуском и сканированием, а одномерной - метод "золотого сечения" и метод сканирования. Покажем как функционируют эти методы.
Метод сканирования самый простой в реализации, но он единственный который ищет глобальный экстремум. Этот метод заключается, при заданных значениях точности и границах, перебором всех значений переменных и из всех вычисленных значений выбирается лучший.
Метод покоординатного спуска заключается в нахождении экстремума поочередно по каждой переменной.
Пусть задана функция двух переменных, линии равного уровня которой изображены на рисунке 6.2.

Рисунок 6.2 - Метод покоординатного спуска
Из некоторой начальной точки Х0= (х1, х2) производится поиск минимума вдоль направления оси х1 с получением точки Х0. В этой точке касательная к линии равного уровня параллельна оси х1. Затем из точки Х0 производится поиск минимума вдоль направления оси х2 с получением точки Х1. Следующие итерации выполняются аналогично. Для минимизации функции F (x) вдоль осевых направлений может быть использован любой из методов одномерной оптимизации.
Приведем описание метода “золотого сечения”.
Пусть экстремум локализован в интервале [x1,x3] (рисунок 6.5).
Алгоритм поиска экстремума складывается из следующих этапов:
а) вычисляются и запоминаются значения функции F (x) на концах исходного интервала [x1,x4], то есть значения F (x1) и F (x4);
б) вычисляются и запоминаются значения функции F (x2), где
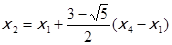 ;
;
в) вычисляются и запоминаются значения функции F (x3), где
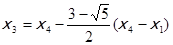
 ;
;
г) по найденным значениям F (x1), F (x2), F (x3) и F (x4) определяется интервал, в котором локализован экстремум, состоящий из двух интервалов l1 и l2 неравной длины.
д) внутри большого интервала l2 находится точка, отстоящая от конца общего интервала l1+l2 на расстоянии.
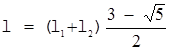 ;
;
е) в этой точке рассчитывается значение функции F (x), после чего снова выбирается сокращенный подинтервал в интервале l1+l2, локализующий экстремум, то есть вычисления повторяются, начиная с пункта.
г) до тех пор, пока не будет получена заданная точность нахождения положения экстремума.
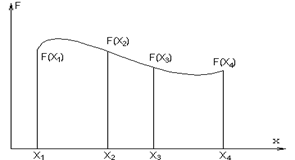
Рисунок 6.3 - Одномерный поиск методом “золотого сечения”
 2020-01-15
2020-01-15 139
139








