2020-01-15
83
Пусть функция полезности наборов из двух товаров 
имеет вид 
, где
.
· Найти набор товаров, который имеет такую же полезность, как набор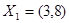 
и количество второго товара равно 1.
· Для набора 
найти предельные полезности первого и второго товаров.
· В наборе 
количество первого товара увеличивается на 0,1, а второго уменьшается на 0,2. Найти приближённое изменение полезности.
РЕШЕНИЕ
1. Функция полезности имеет вид: 
. Найдём полезность набор :
Кривая безразличия 
определяет все наборы товаров, которые имеют такую же полезность как набор . Из этого уравнения можно найти набор товаров, в котором количества второго товара равно 
, подставив это значение в уравнение кривой безразличия 
, 
. Таким образом, наборы 
и 
безразличны для потребителя.
2. Найдём частные производные функции полезности 
Предельная полезность первого товара в наборе равна значению частной производной 
в точке (3,8):
.
Предельная полезность второго товара в наборе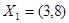 
равна значению частной производной 
в точке (3,8):
Найдём изменение полезности, если количество первого товара увеличивается на 0,1, т.е. 
, а количество второго товара уменьшается на 0,2, т.е.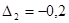 
. Приближённое изменение полезности вычислим по формуле
.
Следовательно, полезность набора , равная 
, увеличивается на 0,0065. Таким образом, полезность нового набора 
