2020-01-15
181
Для высокой скорости:
; 
; 
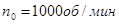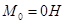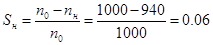
Из соотношения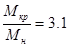 
находим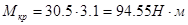 
Найдём критическое скольжение:
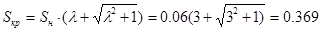, где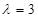 
Найдём частоту вращения при критическом моменте по формуле:
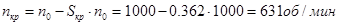
Дли низкой скорости
; 
; 
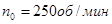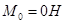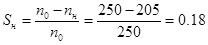
Из соотношения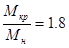 
находим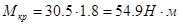 
Найдём критическое скольжение:
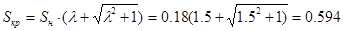, где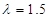 
Найдём частоту вращения при критическом моменте по формуле:
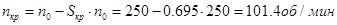
Найдём критический момент для низкой скорости в генераторном режиме по формуле:
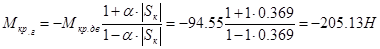, где 
Для расчета механических характеристик (МХ) будем использовать уточненную формулу Клосса, т.к. выбранный двигатель меньше 100 кВт.
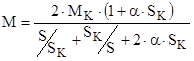, Н×м.
Неизвестные параметры отдельно для высокоскоростной и низкоскоростной обмоток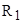 
, 
, 
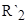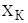получим из формулы критического момента 
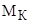и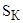 
. Приближенно примем, что 
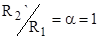, т.е.
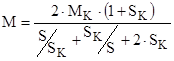(5.1)
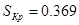. Затем из формулы 
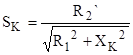, учитывая, что 
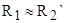найдем 
:
,
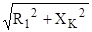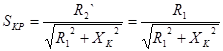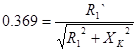, отсюда 
.
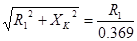Теперь подставим полученное выражение в формулу критического момента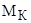 
в двигательном режиме, а также известные паспортные данные:
;
.
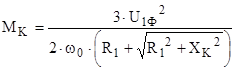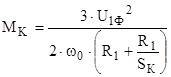Выразим 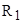из полученного выражения:
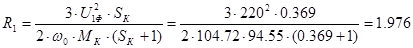Ом.
Из уравнения критического скольжения выразим значение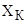 
;
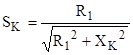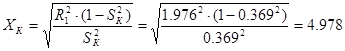Ом.
Для низкоскоростной обмотки расчет проводится аналогичным образом. После расчета мы получили, что: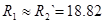 
Ом,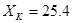 
Ом. На низкоскоростной обмотке при рекуперативном торможении критический момент не вписывается в диапазон 
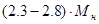, потому что при расчёте было принято допущение 
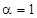, то есть 
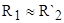. Следовательно, для низкоскоростной обмотки данное допущение неприемлемо. Из справочных данных следует, что кратности пускового и критического момента для низкоскоростной обмотки одинаковы: 
, 
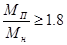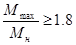. Примем допущение, что 
.
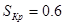Из справочной литературы определим критические моменты:
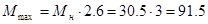Н×м;
С учётом значений критических моментов и скольжения по формуле Клосса методом последовательных приближений определим коэффициент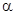 
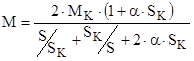, Н×м;
.
Из уравнения для критического скольжения определим подкоренное выражение
.
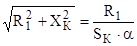Подставим подкоренное выражение в формулу критического момента, откуда определим сопротивление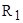 
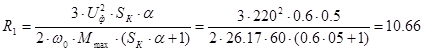Ом.
Приведённое сопротивление ротора
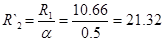Ом.
Реактивное сопротивление
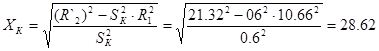Ом.
По формуле Клосса строим ЕМХ для обеих обмоток (рисунок 5.1).
