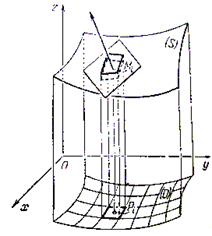
Пусть поверхность  задана явным уравнением
задана явным уравнением  , причём
, причём 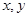 изменяются в квадрируемой области
изменяются в квадрируемой области  на плоскости
на плоскости  , и
, и  в этой области имеет непрерывные частные производные
в этой области имеет непрерывные частные производные  и
и  . Разложим область
. Разложим область  с помощью сетки кривых на элементы
с помощью сетки кривых на элементы  . Рассмотрим
. Рассмотрим  .Если построить на контуре этой частичной области цилиндрическую поверхность с образующими, параллельными оси
.Если построить на контуре этой частичной области цилиндрическую поверхность с образующими, параллельными оси  , то она вырежет на поверхности
, то она вырежет на поверхности  элемент
элемент  . Элемент
. Элемент  соответствует элементу
соответствует элементу  . Точка
. Точка  соответствует точке
соответствует точке 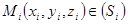 , где
, где  . Проведём в точке
. Проведём в точке  касательную плоскость. Упомянутая цилиндрическая поверхность на этой плоскости вырежет элементарную фигуру
касательную плоскость. Упомянутая цилиндрическая поверхность на этой плоскости вырежет элементарную фигуру  , площадь которой
, площадь которой 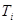 служит приближением к площади элемента
служит приближением к площади элемента  . Сумму
. Сумму 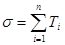 можно считать приближением к площади поверхности
можно считать приближением к площади поверхности  . Площадь
. Площадь  при стремящихся к нулю диаметров всех элементов
при стремящихся к нулю диаметров всех элементов  или
или  . Отсюда
. Отсюда  , где
, где  - угол нормали к поверхности с осью
- угол нормали к поверхности с осью  . Если
. Если  удовлетворяет точке
удовлетворяет точке  , то для площадей плоских фигур
, то для площадей плоских фигур  и
и  имеем
имеем  , откуда
, откуда 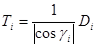 . Получаем интегральную сумму
. Получаем интегральную сумму  . Исходя из того, что
. Исходя из того, что 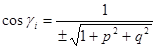 , площадь
, площадь  .
.
Площадь поверхности в общем случае
Рассмотрим простую гладкую поверхность  , заданную параметрически. Для каждой точки
, заданную параметрически. Для каждой точки  поверхности явное уравнение
поверхности явное уравнение  заменяется явным же уравнением
заменяется явным же уравнением  или
или  . Отсюда следует, что вся поверхность
. Отсюда следует, что вся поверхность  разлагается на конечное число кусков
разлагается на конечное число кусков  . Вычислим площадь
. Вычислим площадь  .
.  .
.  .
.
Замечание: Перейдём от параметров  с областью изменения
с областью изменения  к параметрам
к параметрам  с областью изменения
с областью изменения  по формулам
по формулам  ,
,  . Тогда поверхность выразится новыми уравнениями
. Тогда поверхность выразится новыми уравнениями  ,
,  ,
, 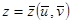 . Обозначим
. Обозначим 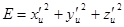 ,
,  ,
,  - так называемые гауссовы коэффициенты. Так как
- так называемые гауссовы коэффициенты. Так как  , то
, то  .
.
Выражение  называют элементом площади в криволинейных координатах.
называют элементом площади в криволинейных координатах.
Пример: Найти площадь частей сферической поверхности  , вырезанных из неё цилиндром
, вырезанных из неё цилиндром 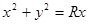 .
.
Решение.  ,
,  ,
,  , тогда
, тогда  , причём областью интегрирования служит круг, ограниченный окружностью
, причём областью интегрирования служит круг, ограниченный окружностью 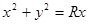 .
.
В полярных координатах получим  . Проинтегрировав, получим
. Проинтегрировав, получим  .
.
В сферических координатах, так как  ,
,  ,
,  , то
, то  .
.
Тройной интеграл
Масса тела. Объём
Пусть дано некоторое тело  , заполненное массами, и в каждой точке
, заполненное массами, и в каждой точке  известна плотность
известна плотность  распределения этих масс. Требуется определить всю массу
распределения этих масс. Требуется определить всю массу  тела.
тела.
Разложим тело  на ряд частей:
на ряд частей:  . Точка
. Точка  . Пусть в пределах части
. Пусть в пределах части  плотность постоянна и равна
плотность постоянна и равна  в выбранной точке. Тогда масса
в выбранной точке. Тогда масса  , масса всего тела
, масса всего тела  . Если диаметры
. Если диаметры  всех частей стремятся к нулю, то
всех частей стремятся к нулю, то  или
или  . Последнее выражение называется тройным интегралом.
. Последнее выражение называется тройным интегралом.
Пусть дана функция  в данном теле
в данном теле  .
.
Если функция  , то
, то  , где
, где  есть объём данного тела
есть объём данного тела
 . Вычисление тройного интеграла можно выполнить с помощью трёх последовательных простых интегрирований.
. Вычисление тройного интеграла можно выполнить с помощью трёх последовательных простых интегрирований.
Пример:
1). Вычислить интеграл  , распространённый на тетраэдр
, распространённый на тетраэдр  , ограничиваемый плоскостями
, ограничиваемый плоскостями  ,
,  ,
,  и
и  (чертёж). Решение: Запишем границы изменения каждой из переменных
(чертёж). Решение: Запишем границы изменения каждой из переменных
 , отсюда
, отсюда





 .
.
Итак,  .
.
 2020-01-15
2020-01-15 326
326








