Выражение площади с помощью криволинейных интегралов
Запишем сначала формулу Грина:  .
.
Если функции P и Q в формуле Грина подобрать так, чтобы  , то двойной интеграл приведётся к площади D.
, то двойной интеграл приведётся к площади D.
Если  и
и 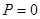 , то
, то  ,
,
если  и
и  , то
, то  ,
,
если  и
и 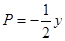 , то
, то  . Последняя формула является наиболее употребительной.
. Последняя формула является наиболее употребительной.
Пример: Найти площадь эллипса с полуосями a и b. Воспользуемся параметрическими уравнениями эллипса:  ,
, 
 . Тогда
. Тогда  .
.
Приложения к физическим задачам

Работа силового поля. Пусть в каждой точке M плоскости xy на помещённую в неё единицу массы действует определённая сила  . Данная плоскость называется силовым полем, а сила
. Данная плоскость называется силовым полем, а сила  - напряжением поля. Из рисунка видно
- напряжением поля. Из рисунка видно  ,
, 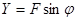 .
.
Пусть точка M (x,y) движется и описывает некоторую непрерывную кривую (K). Вычислим работу A, которую при этом движении совершают силы поля. В случае прямолинейного движения 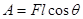 , где
, где

В случае непрямолинейного движения и непостоянной силы станем определять положение точки M на кривой (K) длиной s дуги AM. Тогда  . Просуммируем, работа выразится криволинейным интегралом первого типа:
. Просуммируем, работа выразится криволинейным интегралом первого типа:  . Пусть
. Пусть  - угол между направлением элемента
- угол между направлением элемента  и осью x, тогда
и осью x, тогда  . Окончательно работа силового поля выразится криволинейным интегралом второго типа:
. Окончательно работа силового поля выразится криволинейным интегралом второго типа:  .
.
Плоское установившееся движение несжимаемой жидкости.

При таком движении все частицы, лежащие на одной вертикали к некоторой плоскости, имеют одну и ту же скорость. Скорость  частицы жидкости зависит только от положения частицы, но не от времени.
частицы жидкости зависит только от положения частицы, но не от времени.
Если обозначить угол, составленный вектором  с осью x, через
с осью x, через  , а проекции этого вектора на координатные оси – через
, а проекции этого вектора на координатные оси – через  и
и  , то
, то 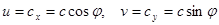 . Количество Q жидкости, протекающей через кривую (K) в определённую от неё сторону в единицу времени, запишется в виде криволинейного интеграла первого типа
. Количество Q жидкости, протекающей через кривую (K) в определённую от неё сторону в единицу времени, запишется в виде криволинейного интеграла первого типа  .
.
Так как  , то
, то  . Перейдём к криволинейному интегралу второго типа
. Перейдём к криволинейному интегралу второго типа  .
.
Поверхностные интегралы
 2020-01-15
2020-01-15 106
106








