Рассмотрим вопрос о вычислении площади поверхности вращения. Вычислим площадь поверхности вращения, считая её существующей и обладающей свойством аддитивности.
Пусть имеем на плоскости xy (именно в верхней полуплоскости) некоторую кривую AB, заданную уравнением вида 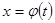 ,
, 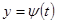 ,
, 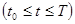 , (10)
, (10)
Где 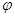 и
и 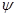 - функции от параметра, непрерывные вместе со своими производными. Для простоты будем предполагать её незамкнутой и лишённой кратных точек. Нам удобно ввести в качестве параметра дугу s, отсчитываемую от точки
- функции от параметра, непрерывные вместе со своими производными. Для простоты будем предполагать её незамкнутой и лишённой кратных точек. Нам удобно ввести в качестве параметра дугу s, отсчитываемую от точки 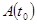 , и перейти к представлению
, и перейти к представлению 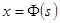 ,
, 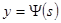 ,
, 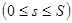 (11)
(11)
Параметр s изменяется здесь от 0 до S, если через S обозначить длину всей кривой AB.
Задача состоит в определении площади Q поверхности, полученной от вращения кривой AB вокруг оси x. Роль независимой переменной играет 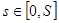 .
.
Если выделить элемент ds кривой (чертёж 12), то его приближённо можно принять за прямолинейный и вычислять соответствующий ему элемент площади 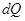 как площадь усечённого конуса с образующей ds и радиусами основания y и y+dy. Тогда, по известной из школьного курса формуле,
как площадь усечённого конуса с образующей ds и радиусами основания y и y+dy. Тогда, по известной из школьного курса формуле, 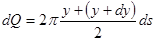 . Впрочем, это ещё не та формула, к которой мы стремимся – произведение
. Впрочем, это ещё не та формула, к которой мы стремимся – произведение 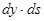 двух бесконечно малых надо отбросить. Мы придём к линейной относительно
двух бесконечно малых надо отбросить. Мы придём к линейной относительно 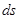 формуле
формуле 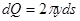 , откуда уже, «суммируя», окончательно получим
, откуда уже, «суммируя», окончательно получим 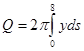 (12)
(12)
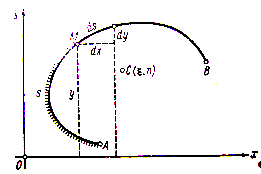
где под y надлежит разуметь фигурирующую в (11) функцию 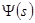 .
.
Если вернуться к общему параметрическому заданию (10) нашей кривой, то, произведя в предшествующем интеграле замену переменной, преобразуем его к виду (чертёж 12)
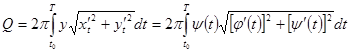 . (12а)
. (12а)
В частности, если кривая задана явным уравнением 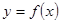
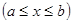 , так что в роли параметра оказывается x, будем иметь:
, так что в роли параметра оказывается x, будем иметь:
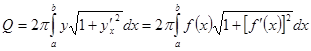 . (12б)
. (12б)
Примеры:
1). Определить площадь поверхности шарового пояса.
Пусть полукруг, описанный около начала радиусом r, вращается вокруг оси x. Из уравнения круга имеем 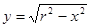 ; далее,
; далее, 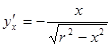 ,
, 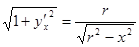 ,
, 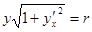 . В таком случае площадь поверхности пояса, описанного дугой, концы которой имеют абсциссы
. В таком случае площадь поверхности пояса, описанного дугой, концы которой имеют абсциссы 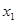 и
и 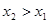 , по формуле (12б) будет
, по формуле (12б) будет 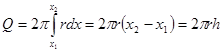 , где h – высота пояса. Таким образом, площадь поверхности шарового пояса равна произведению окружности большого круга на высоту пояса. В частности, при
, где h – высота пояса. Таким образом, площадь поверхности шарового пояса равна произведению окружности большого круга на высоту пояса. В частности, при 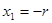 и
и 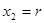 , т.е. при
, т.е. при 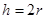 , получаем площадь всей шаровой поверхности
, получаем площадь всей шаровой поверхности 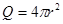 .
.
2). Найти площадь поверхности, образованной вращением дуги циклоиды 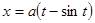 ,
, 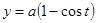 .
.
Так как 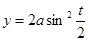 ,
, 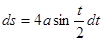 , то
, то
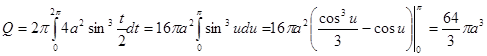 .
.
 2020-01-15
2020-01-15 118
118








