Система нелінійних рівнянь

Курсова робота

З дисципліни «Чисельні методи»

Тема проекту: «Системи нелінійних рівнянь»

 

Виконала:

студентка групи КН-II-2

Омельченко Ю.В.

 

 

Київ 2008

Зміст

Вступ

Розділ 1 Чисельні методи розв’язання систем нелінійних рівнянь

1.1 Нелінійні рівняння

1.2 Система нелінійних рівнянь

1.3 Метод простих ітерацій

1.4 Метод Ньютона

1.5 Модифікований метод Ньютона

Розділ 2 Практичне використання методів розв’язання систем нелінійних рівнянь

2.1 Розв’язання систем нелінійних рівнянь у пакеті Mathcad

2.2 Розв’язання систем нелінійних рівнянь у пакеті Excel

2.3 Розв’язання систем нелінійних рівнянь на мові С++

Висновок

Список використаної літератури

 

Вступ

З розвитком нової обчислюваної техніки інженерна практика наших днів більш часто зустрічається з математичними задачами, точне вирішення яких отримати досить складно чи неможливо. В цих випадках звичайно застосовують ті чи інші наближенні обчислення. Ось чому наближені та чисельні методи математичного аналізу отримали за останні роки широкий розвиток і набули виключно важливе значення.

Нові обчислювальні засоби спричинили переоцінку відомих методів вирішення задач з точки зору доцільності їх реалізації на ЕОМ і стимулювали створення більш ефективних.

Предметом вивчення обчислювальної математики є чисельні методи вирішення задач математичного аналізу: вивчення алгоритму метода, умови збіжності ітераційних методів, вивчення границь використання методів, дослідження оцінки похибки методів і обчислень. Головним розділом обчислювальної математики є реалізація чисельних методів на ЕОМ, тобто створення програми для потрібного алгоритму і вирішення конкретної задачі за допомогою складеної програми.

У даній курсовій роботі я розгляну чисельні методи розв’язання систем нелінійних рівнянь. Серед них метод простих ітерацій та метод Ньютона в різних модифікаціях. Ці методи реалізовані в Mathcad, Excel та на мові програмування С++.

Розділ 1 Чисельні методи розв’язання систем нелінійних рівнянь

Нелінійні рівняння

Нелінійними рівняннями називаються рівняння виду

. (1.1.1)

Тут  - нелінійна функція:

– Нелінійна алгебраїчна функція виду;

– Трансцендентні функції – тригонометричні, обернені тригонометричні, логарифмічні, показникові и гіперболічні функції;

– комбінування цих функцій .

Розв’язком нелінійного рівняння (1.1.1) є така точка 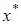, яка при підстановці у рівняння (1.1.1) перетворює його у тотожність. На практиці не завжди вдається підібрати такий розв’язок. В цьому випадку, розв’язок рівняння (1.1.1) знаходиться із застосуванням наближених (чисельних) методів. Тоді розв’язком нелінійного рівняння (1.1.1) буде така точка 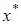, при підстановці якої у рівняння (1.1.1) останнє буде виконуватися з певним степенем точності, тобто 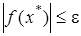, де  - мала величина. Знаходження таких розв’язків складає основу чисельних методів і обчислюваної математики.

Розв’язання нелінійних рівнянь складається з двох етапів:

1) відокремлення коренів;

2) уточнення коренів нелінійних рівнянь.

На першому етапі необхідно дослідити рівняння і з’ясувати є корні чи ні. Якщо корні є, то скільки їх, і потім з’ясувати інтервали, в кожному з яких знаходиться єдиний корінь.

 

Перший спосіб відокремлення коренів – графічний. Виходячи із рівняння (1.1.1), можна побудувати графік функції . Тоді точка перетину графіка з віссю абсцис є приближенням значення кореня. Якщо  має складний вигляд, то представимо її у вигляді різниці двох функцій . Так як , то виконується рівність . Побудуємо два графіки , . Значення 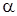 - приблизне значення кореня (Рис.1), яке є абсцисою точки перетину двох графіків.

Другий спосіб відокремлення коренів нелінійних рівнянь – аналітичний. Процес відокремлення коренів нелінійних рівнянь базується на наступних теоремах.

Теорема 1. Якщо функція  неперервна на відрізку  і змінює на кінцях відрізка знак (тобто 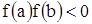), то на  міститься хоча б один корінь.

Теорема 2. Якщо функція  неперервна на відрізку , виконується умова вигляду  і похідна  зберігає знак на , то на відрізку міститься єдиний корінь.

Теорема 3. Якщо функція  є многочленом  степені і на кінцях відрізка  змінюється знак, то на  міститься непарна кількість коренів (якщо похідна  зберігає знак на , то корінь єдиний). Якщо на кінцях відрізка  функція не змінює знак, то рівняння (1.1.1) або не має коренів на , або має парну кількість коренів.

При аналітичному методі дослідження необхідно з’ясувати інтервали монотонності функції . Для цього необхідно обчислити критичні точки , тобто точки, у яких перша похідна  дорівнює нулю чи не існує. Тоді вся числова вісь розбивається на інтервали монотонності 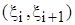. На кожному із них з’ясовується знак похідної , де . Потім виділяємо ті інтервали монотонності, на яких функція  змінює знак. На кожному із цих інтервалів для пошуку кореня використовуються методі уточнення коренів.

 

Система нелінійних рівнянь

Система нелінійних рівнянь має вигляд:

 

 (1.2.1)

 

Тут  - невідомі змінні, а система (1.2.1) називається звичайною системою порядку , якщо хоча б одна із функцій  нелінійна.

Розв’язання систем нелінійних рівнянь – одна із складних задач обчислювальної математики. Складність полягає у тому, щоб з’ясувати: чи має система розв’язок, і, якщо – так, то скільки. Уточнення розв’зків у заданій області – більш проста задача.

Нехай функції  визначені в областях . Тоді область 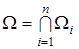 і буде тією областю, де можна знайти розв’язок. Найбільш відомими методами уточнення розв’язків є метод простих ітерацій та метод Ньютона.