Программирования
Предположим, что цена игры положительна (u > 0). Если это не так, то согласно свойству 6 всегда можно подобрать такое число с, прибавление которого ко всем элементам матрицы выигрышей даёт матрицу с положительными элементами, и следовательно, с положительным значением цены игры. При этом оптимальные смешанные стратегии обоих игроков не изменяются.
Свойство 1. Тройка (хо, yо, u) является решением игры G = (Х,Y,А) тогда и только тогда, когда (хо, yо, кu +а) является решением игры G(Х,Y,кА+а), где а – любое вещественное число, к > 0.
Свойство 2. Для того, чтобы хо = (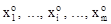 ) была оптимальной смешанной стратегией матричной игры с матрицей А и ценой игры u, необходимо и достаточно выполнение следующих неравенств
) была оптимальной смешанной стратегией матричной игры с матрицей А и ценой игры u, необходимо и достаточно выполнение следующих неравенств
 (j =
(j = 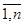 )
) 
Аналогично для игрока 2: чтобы yо = ( ,...,
,...,  ,...,
,...,  ) была оптимальной смешанной стратегией игрока 2 необходимо и достаточно выполнение следующих неравенств:
) была оптимальной смешанной стратегией игрока 2 необходимо и достаточно выполнение следующих неравенств:
 (i =
(i =  )
) 
Из последнего свойства вытекает: чтобы установить, является ли предполагаемые (х, y) и u решением матричной игры, достаточно проверить, удовлетворяют ли они неравенствам (*) и (**). С другой стороны, найдя неотрицательные решения неравенств (*) и (**) совместно со следующими уравнениями
 ,
, 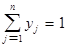

получим решение матричной игры.
Итак, пусть дана матричная игра с матрицей А порядка m х n. Согласно свойству 7 оптимальные смешанные стратегии х = (х1,..., хm), y = (y1,..., yn) соответственно игроков 1 и 2 и цена игры u должны удовлетворять соотношениям.




Разделим все уравнения и неравенства в (4.4) и (4.5) на u (это можно сделать, т.к. по предположению u > 0) и введём обозначения:

 ,
, 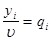
 ,
,
Тогда (1) и (2) перепишется в виде:
 ,
,  ,
, 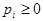 ,
,  ,
,
 ,
, 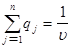 ,
,  ,
,  .
.
Поскольку первый игрок стремится найти такие значения хi и, следовательно, pi, чтобы цена игры u была максимальной, то решение первой задачи сводится к нахождению таких неотрицательных значений pi  , при которых
, при которых
 ,
,  .
. 
Поскольку второй игрок стремится найти такие значения yj и, следовательно, qj, чтобы цена игры u была наименьшей, то решение второй задачи сводится к нахождению таких неотрицательных значений qj,  , при которых
, при которых
 ,
,  .
. 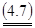
Формулы (3) и (4) выражают двойственные друг другу задачи линейного программирования (ЛП).
Решив эти задачи, получим значения pi  , qj
, qj  и u.Тогда смешанные стратегии, т.е. xi и yj получаются по формулам:
и u.Тогда смешанные стратегии, т.е. xi и yj получаются по формулам:


Решение задач
Пример 5: Найти решение игры, определяемой матрицей.

Решение.
Составим теперь пару взаимно-двойственных задач:


Решим вторую из них
| Б.п. | q1 | q2 | q3 | q4 | q5 | q6 | Решение | å | Отношение |

| -1 | -1 | -1 | 0 | 0 | 0 | 0 | -3 | |
 q4 q4
| 1 | 2 | 0 | 1 | 0 | 0 | 1 | 5 | — |
| q5 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 4 | 
|
| q6 | 2 | 1 | 0 | 0 | 0 | 1 | 1 | 5 | — |
| Б.п. | q1 | q2 | q3 | q4 | q5 | q6 | Решение | å | Отношение |

| 0 | -1 | 0 | 0 | 1 | 0 | 1 | 1 | |
  q4 q4
| 1 | 2 | 0 | 1 | 0 | 0 | 1 | 5 | 
|
| q3 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 4 | — |
| q6 | 2 | 1 | 0 | 0 | 0 | 1 | 1 | 5 | 
|
| Б.п. | q1 | q2 | q3 | q4 | q5 | q6 | Решение | å | Отношение |

| 
| 0 | 0 | 
| 1 | 0 | 
| 
| |
| q2 | 
| 1 | 0 | 
| 0 | 0 | 
| 
| |
| q3 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 4 | |
| q6 | 
| 0 | 0 | 
| 0 | 1 | 
| 
|
Из оптимальной симплекс-таблицы следует, что 
(q1, q2, q3) = (0;  ; 1),
; 1),
а из соотношений двойственности следует, что
(p1, p2, p3) = (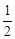 ; 1; 0).
; 1; 0).
Следовательно, цена игры с платёжной матрицей А1 равна
 .
.  ,
,
а игры с платёжной матрицей А:
 .
.
При этом оптимальные стратегии игроков имеют вид:
Х = (х1, х2, х3) = (uр1; uр2; uр3) =  =
= 
Y = (y1, y2, y3) = (uq1; uq2; uq3) = 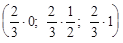 =
=  .
.
 2020-01-15
2020-01-15 80
80








