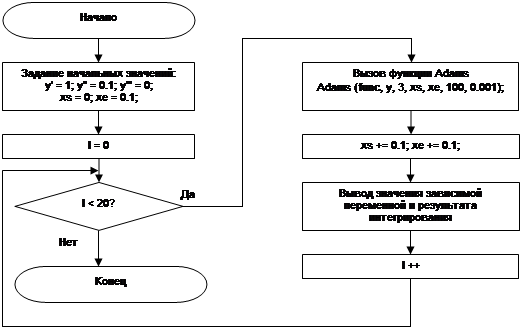
Блок-схема функции Adams из программы 17.c
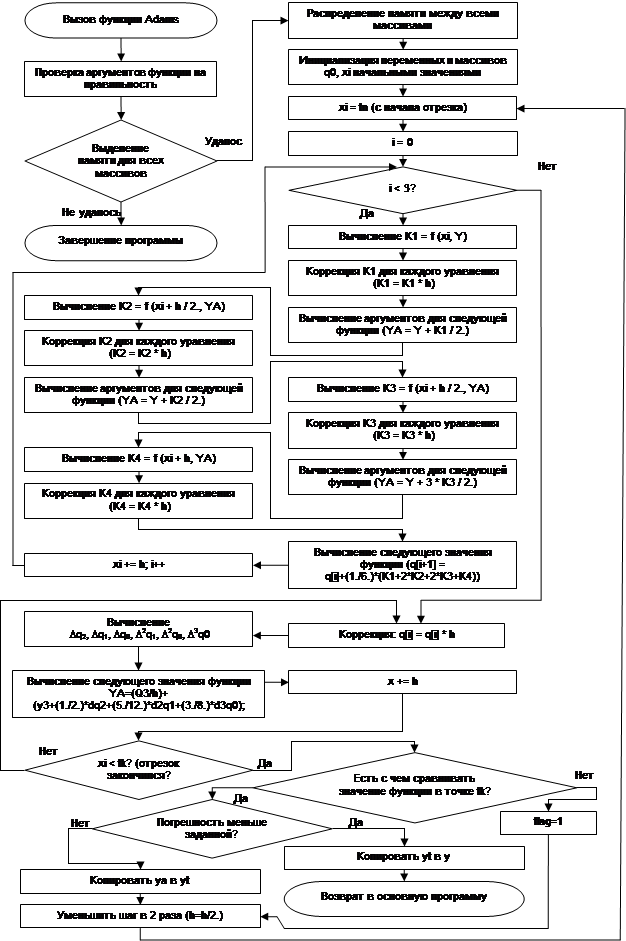
Листинг программы 17.c
// Задача 17. Численное интегрирование системы дифференциальных уравнений
// методом Адамса. Программа рассчитана на компиляцию в Micro$oft C 6.00
// или Borland C 3.1+
// (C) 2004 REPNZ. All rights reserved. Release date is 2.04.2004
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
void func (double *y, double *ys, double t)
{ // функция вычисления правых частей уравнений
ys[0] = y[1]; // ys[1]-первая производная; ys[2]-вторая и т.д.
ys[1] = y[2]; // t-независимый аргумент
ys[2] = 5 + t * t - y[0] - 3. * y[1] - 2. * y[2];
}
void Adams (
void f (double *y, double *ys, double x),
// Функция вычиления правых частей системы
double *y, // Массив размера n значений зависимых переменных
int n, // Массив размера n значений производных
double tn, // Начало интервала интегрирования
double tk, // Конец интервала интегрирования
int m, // Начальное число разбиений отрезка интегрирования
double eps) // Относительная погрешность интегрирования
{
double *k1, *k2, *k3, *k4; // Для метода Рунге-Кутта
double *q0, *q1, *q2, *q3; // Значение производных Для метода Адамса
double *ya; // Временный массив
double *y0, *y1, *y2, *y3; // Значения функции для метода Адамса
double h; // Шаг интегрирования
double xi; // Текущее значение независимой переменной
double eps2; // Для оценки погрешности
double dq2, dq1, dq0, d2q1, d2q0, d3q0; // приращения
int flag = 0; // 0, пока идёт первый просчёт
int i, j; // Индексы
if (m < 4) m = 4; // Минимум 4 отрезка
if (tn >= tk)
{ printf ("\nНеправильные аргументы\n");
abort (); // Неправильные аргументы
}
// Выделяем память для массивов с переменными
if ((k1 = malloc ((4 + 4 + 4 + 1) * n * sizeof (double))) == 0)
{ printf ("\nОшибка распределения памяти\n");
abort (); // Прервать, если не удалось
}
// Распределяем память между массивами:
// Для метода Рунге-Кутта 4 порядка
k2 = k1 + n; k3 = k2 + n; k4 = k3 + n;
// 4 пердыдущих значения функции
y0 = k4 + n; y1 = y0 + n; y2 = y1 + n; y3 = y2 + n;
// Для временного массива сбора данных
ya = y3 + n;
// Для метода Адамса
q0 = ya + n; q1 = q0 + n; q2 = q1 + n; q3 = q2 + n;
h = (tk - tn) / m; // Шаг
eps = fabs (eps); // Абсолютное значение погрешности
start: // Отсюда начинаются вычисления
xi = tn; // Начало промежутка
// Вычисляем значения функции y0...y3, т.е. y[i-3]... y[0]
// Первое значение системы уравнений уже дано: y...
///////////////////////////////////////////////////////////////////////
// - Метод Рунге-Кутта 4 порядка - //
///////////////////////////////////////////////////////////////////////
for (j = 0; j < n; j++) y0[j] = y[j]; // Копируем его в y0
f (y0, q0, xi); // Заполняем q0, основываясь на значениях из y0
for (j = 0; j < n; j++) q0[j] *= h; // Делаем q0
xi += h; // Следующий шаг
//... а остальные 3 добываем с помощью метода Рунге-Кутта 4 порядка.
for (i = 0; i < 3; i++) // i - КАКОЕ ЗНАЧЕНИЕ УЖЕ ЕСТЬ
{ // А ВЫЧИСЛЯЕМ ЗНАЧЕНИЯ Y[i+1]!!!!
// Сначала нужны коэффициенты k1
// Элемент y[i, j] = y0 + (i * n) + j = y0[i * n + j]
f (&y0[i * n], k1, xi); // Вычислим f(xi, yi) = k1 / h
// И для каждого дифференциального уравнения системы проделываем
// операции вычисления k1, а также подготовки в ya аргумента для
// вычисления k2
for (j = 0; j < n; j++)
{
k1[j] *= h; // Вычислим наконец-то k1
ya[j] = y0[i*n+j] + k1[j] / 2.;
// И один из аргументов для функции
} // вычисления k2
f (ya, k2, xi + (h / 2.)); // Вычислим f(xi,yi) = k2 / h
for (j = 0; j < n; j++)
{ // Вычислим наконец-то k2
k2[j] *= h;
ya[j] = y0[i*n+j] + k2[j] / 2.; // И один из аргументов для функции
} // вычисления k3
f (ya, k3, xi + h / 2.); // Вычислим f(xi,yi) = k3 / h
for (j = 0; j < n; j++)
{
k3[j] *= h; // Вычислим наконец-то k3
ya[j] = y0[i*n+j] + k3[j]; // И один из аргументов для функции
} // вычисления k4
f (ya, k4, xi + h); // Вычислим f(xi,yi) = k4 / h
for (j = 0; j < n; j++) k4[j] *= h; // Вычислим наконец-то k4
// Надо вычислить приращение каждой функции из n
for (j = 0; j < n; j++) // Вычисляем следующее значение
// функции
// Y[i+1] = Yi +...
y0[(i+1)*n+j] = y0[i*n+j] + (k1[j] + 2. * k2[j] + 2 * k3[j] + k4[j]) / 6.;
// И новое значение q[i+1]
f (&y0[(i+1)*n], &q0[(i+1)*n], xi); // qi = f (xi, yi);
for (j = 0; j < n; j++) q0[((i+1)*n)+j] *= h;
xi += h; // Следующий шаг }
///////////////////////////////////////////////////////////////////////
// - Метод Адамса - //
///////////////////////////////////////////////////////////////////////
// Итак, вычислены 4 первых значения. Этого достаточно для начала метода
// Адамса для шага h.
// B y0...y3 лежат 4 значения функций (_НЕ_ПРОИЗВОДНЫХ!!!).
// A в q0...q3 лежат значения _производных_ этих функций, умноженных на h
// q0..q3, а также y0..y3 представляют собой очереди с 4 элементами
again: // Вычисляем новое значение функции Yi (Это Y[i+1])
for (j = 0; j < n; j++)
{ // Все приращения
dq2 = q3[j] - q2[j]; dq1 = q2[j] - q1[j]; dq0 = q1[j] - q0[j];
d2q1 = dq2 - dq1; d2q0 = dq1 - dq0;
d3q0 = d2q1 - d2q0;
// новое значение функции (в ya пока что)
ya[j] = y3[j] + (q3[j] + (dq2 / 2.) + (5. * d2q1 / 12.) + (3. * d3q0 / 8.));
// Сдвигаем все массивы на 1 вперёд и добавляем в очередь новое
// значение функции
y0[j] = y1[j]; y1[j] = y2[j]; y2[j] = y3[j]; y3[j] = ya[j];
// Просто сдвигаем q, ничего пока что не добавляя
q0[j] = q1[j]; q1[j] = q2[j]; q2[j] = q3[j];
}
// В очередь в качестве q3 ложим новое значение
f (y3, q3, xi); // q3 = f (xi, y3);
for (j = 0; j < n; j++) q3[j] *= h; // Вычислить q3
// Очередное значение функции вычислено. Следующиий шаг
xi += h;
// Продолжить интегрирование?
if (xi < tk) goto again; // Да.
// Если первый раз здесь, то просчитать ещё раз с шагом h/2
if (flag == 0)
flag = 1; // Сравнивать уже будет с чем
else
{
// Не первый раз - оценить погрешность
// Сейчас в y3 - значение только что вычисленной функции,
// а в y2 - занчение функции, вычисленной с шагом h * 2
// по отношению к текущему
for (j = 0; j < n; j++)
{ eps2 = fabs (((y3[j] - y2[j]) / y2[j]));
if (eps2 > eps) break; // Если погрешность слишком великА
}
if (j == n) // Если всё ОК
{ // Копируем результат
for (j = 0; j < n; j++) y[j] = y3[j];
free (k1); // Освобождаем память
return; // Возвращаемся в main
}
}
// По каким-то причинам выхода из функции не произошло -
// тогда уменьшаем шаг в 2 раза и повторяем
// всё, начиная с метода Рунге-Кутта
h /= 2.; // Уменьшить шаг
goto start; // Повторить расчёт сначала, с новыми параметрами
}
int main ()
{
double y[3], xs, xe;
int i;
y[0] = 1.; y[1] = 0.1; y[2] = 0.; // Начальные условия
xs =.0; xe =.1; // Начало интегрирования
printf ("x = %5.3lg, y(%4.2lg) = %10.3lg\n", xs, xs, y[0]);
for (i = 0; i < 20; i++)
{
Adams (func, y, 3, xs, xe, 10, 1.e-3);
xs += 0.1; xe += 0.1;
printf ("x = %5.3lg, y(%4.2lg) = %10.3lg\n", xs, xs, y[0]);
}
return 0;
}
 2020-01-15
2020-01-15 182
182








