Рассмотрим вращательно-симметричную оптическую систему. Пусть 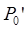 ,
,  и
и  , - точки пересечения луча, выходящего из точки предмета
, - точки пересечения луча, выходящего из точки предмета  , соответственно с плоскостью входного зрачка, плоскостью выходного зрачка и плоскостью параксиального изображения. Если
, соответственно с плоскостью входного зрачка, плоскостью выходного зрачка и плоскостью параксиального изображения. Если  - параксиальное изображение точки
- параксиальное изображение точки  то вектор
то вектор 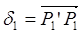 называется аберрацией луча или просто лучевой аберрацией (рис. 2.1).
называется аберрацией луча или просто лучевой аберрацией (рис. 2.1).
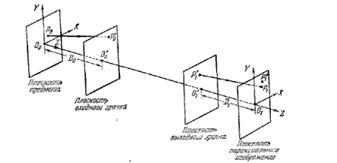
Рис. 2.1. Лучевая аберрация
|
 выходного зрачка и связанный с пучком, который формирует изображение и выходит из точки
выходного зрачка и связанный с пучком, который формирует изображение и выходит из точки 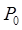 . Если аберрации отсутствуют, то W совпадает со сферой S, центр которой лежит в точке параксиального изображения
. Если аберрации отсутствуют, то W совпадает со сферой S, центр которой лежит в точке параксиального изображения 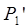 , а сама она проходит через точку
, а сама она проходит через точку  , S называется опорной сферой Гаусса (рис. 2.2).
, S называется опорной сферой Гаусса (рис. 2.2).
Пусть  и
и 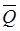 — точки пересечения луча
— точки пересечения луча  с опорной сферой и волновым фронтом W соответственно.
с опорной сферой и волновым фронтом W соответственно.
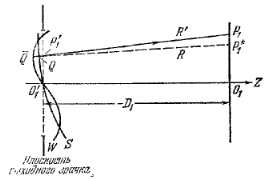
Рис. 2.2.Волновая и лучевая аберрации
Оптическую длину пути Ф =  можно назвать аберрацией волнового элемента в точке Q или просто волновой аберрацией и считать положительной, если
можно назвать аберрацией волнового элемента в точке Q или просто волновой аберрацией и считать положительной, если  и
и  , расположены по разные стороны от Q. В обычных приборах волновые аберрации достигают 40—50 длин волн, однако в приборах, используемых для более точных исследований (например, в астрономических телескопах или микроскопах), они должны быть значительно меньше, порядка долей длины волны.
, расположены по разные стороны от Q. В обычных приборах волновые аберрации достигают 40—50 длин волн, однако в приборах, используемых для более точных исследований (например, в астрономических телескопах или микроскопах), они должны быть значительно меньше, порядка долей длины волны.
Выражения для волновой аберрации легко получить с помощью точечной характеристической функции Гамильтона системы.
Если пользоваться для обозначения оптической длины пути квадратными скобками 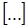 , то
, то
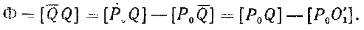 (1)
(1)
Здесь было использовано то обстоятельство, что точки  и
и 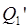 лежат на одном волновом фронте, т.е.
лежат на одном волновом фронте, т.е.  .
.
Введем две прямоугольные системы координат со взаимно параллельными осями, начала которых находятся в осевых точках 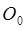 и
и 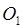 плоскостей предмета и изображения, а оси Z совпадают с осью системы. Точки в пространстве предмета будут рассматриваться в первой системе, а в пространстве изображения — во второй. Z -координаты плоскостей, в которых лежат зрачки, обозначены через
плоскостей предмета и изображения, а оси Z совпадают с осью системы. Точки в пространстве предмета будут рассматриваться в первой системе, а в пространстве изображения — во второй. Z -координаты плоскостей, в которых лежат зрачки, обозначены через 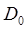 и
и 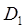 , (на рис 2.1
, (на рис 2.1  ).
).
Согласно (1) волновая аберрация выражается через точечную характеристику V следующим образом:
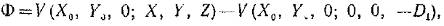 (2)
(2)
где ( ) — координаты точки
) — координаты точки  , и (X,Y,Z) — координаты точки Q. Координаты (X,Y,Z) уже не являются независимыми; они связаны соотношением, учитывающим, что точка Q лежит на опорной сфере, т. е,
, и (X,Y,Z) — координаты точки Q. Координаты (X,Y,Z) уже не являются независимыми; они связаны соотношением, учитывающим, что точка Q лежит на опорной сфере, т. е,
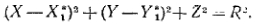 (3)
(3)
Здесь
 (4)
(4)
— координаты точки  параксиального изображения, М — гауссово поперечное увеличение и R — радиус опорной сферы Гаусса
параксиального изображения, М — гауссово поперечное увеличение и R — радиус опорной сферы Гаусса
 . (5)
. (5)
Величину Z в выражении (2) можно исключить с помощыо (3), в результате чего Ф стонет функцией только  ,
, 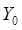 ,
, 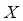 и
и 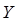 , т. е,
, т. е,

Лучевые аберрации связаны с функцией аберраций Ф (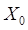 ,
, 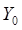 ; X, Y) простыми соотношениями. Из (2) имеем
; X, Y) простыми соотношениями. Из (2) имеем
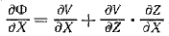 (6)
(6)
Если  ,
, 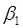 и
и 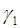 — углы, которые образуют луч
— углы, которые образуют луч 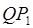 , с осями, а (X, Y, Z) и (
, с осями, а (X, Y, Z) и (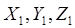 ) — координаты точек
) — координаты точек  и
и  то, на рис. 2.2, получим
то, на рис. 2.2, получим
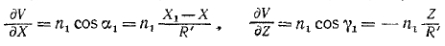 (7)
(7)
где
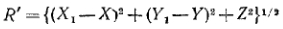 (8)
(8)
есть расстояние от  до
до  , и
, и  — показатель преломления среды в пространстве изображения. Далее из (3) имеем
— показатель преломления среды в пространстве изображения. Далее из (3) имеем
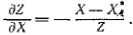 (9)
(9)
Подставляя (7) и (9) в соотношение (6), находим для компонент лучевой аберрации
 (10)
(10)
Последние соотношения являются точными, но стоящая справа величина
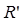 сама зависит от координат точки
сама зависит от координат точки  , т. е. от лучевых аберраций. Тем не менее для большинства практических целей
, т. е. от лучевых аберраций. Тем не менее для большинства практических целей 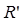 можно заменять на радиус опорной сферы R или на другое приближенное выражение (см. ниже, уравнение (15)). Легко показать, что в силу симметрии задачи величина Ф зависит от четырех переменных, входящих только в трех комбинациях, а именно:
можно заменять на радиус опорной сферы R или на другое приближенное выражение (см. ниже, уравнение (15)). Легко показать, что в силу симметрии задачи величина Ф зависит от четырех переменных, входящих только в трех комбинациях, а именно: 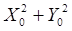 ,
,  и
и  . В самом деле, если ввести в плоскостях XY полярные координаты, т. е. положить
. В самом деле, если ввести в плоскостях XY полярные координаты, т. е. положить
 (11)
(11)
то окажется, что Ф зависит только от 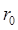 ,
, 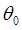 ,
,  и
и  , или, что то же самое, Ф зависит от
, или, что то же самое, Ф зависит от 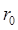 ,
,  ,
, 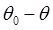 и 0. Предположим теперь, что оси X и Y систем с началами в
и 0. Предположим теперь, что оси X и Y систем с началами в  и
и  поворачивается на один и тот же угол и в одном и том же направлении относительно оси системы.
поворачивается на один и тот же угол и в одном и том же направлении относительно оси системы.
При этом 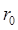 ,
,  ,
, 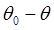 не изменяются, а угол 0 увеличивается на угол поворота. Поскольку функции Ф инвариантна относительно таких поворотов, она не должна зависеть от последней переменной, т. е. зависит только от
не изменяются, а угол 0 увеличивается на угол поворота. Поскольку функции Ф инвариантна относительно таких поворотов, она не должна зависеть от последней переменной, т. е. зависит только от 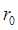 ,
,  , и
, и 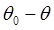 . Следовательно, функции аберраций Ф является функцией трех скалярных произведений
. Следовательно, функции аберраций Ф является функцией трех скалярных произведений
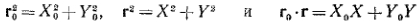 (12)
(12)
двух векторов 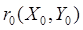 и
и 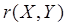 .
.
Отсюда вытекает, что при разложении Ф в ряд по степеням четырех координат нечетные степени будут отсутствовать. Поскольку Ф (0, 0; 0, 0) = 0, то членов нулевой степени тоже не будет. Более того, не будет и членов второй степени, так как, согласно (10), они соответствуют лучевым аберрациям, линейно зависящим от координат, а это противоречит тому, что 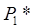 , является параксиальным изображением точки
, является параксиальным изображением точки 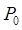 . Таким образом, наше разложение имеет вид
. Таким образом, наше разложение имеет вид
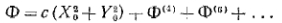 (13)
(13)
где с - константа, а  — полином степени 2k по координатам и содержит их только в виде трех скалярных инвариантов (12). Говорят, что член степени 2k описывает волновую аберрацию порядка 2k. Аберрации наинизшего порядка (2k = - 4) обычно называются первичными аберрациями или аберрациями Зайделя.
— полином степени 2k по координатам и содержит их только в виде трех скалярных инвариантов (12). Говорят, что член степени 2k описывает волновую аберрацию порядка 2k. Аберрации наинизшего порядка (2k = - 4) обычно называются первичными аберрациями или аберрациями Зайделя.
Для оценки порядка величин некоторых выражений и точности наших вычислений удобно ввести параметр 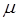 . Этим параметром может служить любая величина первого порядка, скажем, угловая апертура системы. Тогда можно допустить, что все лучи, проходящие через систему, составляют с оптической осью углы О(
. Этим параметром может служить любая величина первого порядка, скажем, угловая апертура системы. Тогда можно допустить, что все лучи, проходящие через систему, составляют с оптической осью углы О(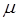 ), где символ О(
), где символ О(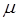 ) означает, что величина угла порядка
) означает, что величина угла порядка 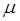 .
.
Оценим погрешность, возникающую при замене 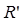 в основном уравнении (10) на величины, не зависящие от
в основном уравнении (10) на величины, не зависящие от  и
и 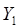 . Из (3) и (5) имеем
. Из (3) и (5) имеем
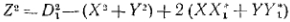 (14)
(14)
тогда вместо (8) можем написать
 (15)
(15)
Соотношения (10) для компонент лучевой аберрации принимают вид
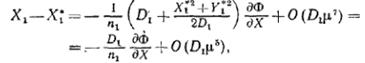 (16)
(16)
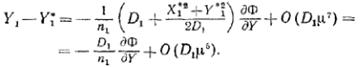 (17)
(17)
 2020-01-15
2020-01-15 191
191








